Solveeit Logo
Login

Question

Question: Zn(OH)₂ is an amphoteric hydroxide and is involved in the following two equilibria in aqueous soluti...

Zn(OH)₂ is an amphoteric hydroxide and is involved in the following two equilibria in aqueous solutions?

Zn(OH)2⇌Zn2+(aq)+2OH−(aq);Ksp=1.2×10−17Zn(OH)_2 \rightleftharpoons Zn^{2+}(aq) + 2OH^-(aq); K_{sp} = 1.2 \times 10^{-17}

Zn(OH)2(s)+2OH−(aq)⇌[Zn(OH)4]2−(aq);Kc=0.12Zn(OH)_2(s) + 2OH^-(aq) \rightleftharpoons [Zn(OH)_4]^{2-}(aq); K_c = 0.12 At what pH the solubility of Zn(OH)2Zn(OH)_2 be minimum?

Answer

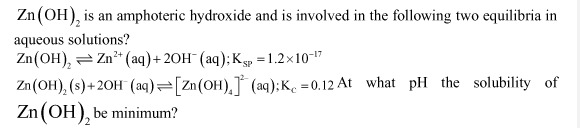
10

Explanation

Solution

The solubility of Zn(OH)2Zn(OH)_2 in aqueous solution is determined by two equilibria:

  1. Dissolution to form simple ions:

    Zn(OH)2(s)⇌Zn2+(aq)+2OH−(aq);Ksp=[Zn2+][OH−]2=1.2×10−17Zn(OH)_2(s) \rightleftharpoons Zn^{2+}(aq) + 2OH^-(aq); K_{sp} = [Zn^{2+}][OH^-]^2 = 1.2 \times 10^{-17}

  2. Dissolution to form a complex anion in the presence of excess hydroxide:

    Zn(OH)2(s)+2OH−(aq)⇌[Zn(OH)4]2−(aq);Kc=[[Zn(OH)4]2−][OH−]2=0.12Zn(OH)_2(s) + 2OH^-(aq) \rightleftharpoons [Zn(OH)_4]^{2-}(aq); K_c = \frac{[[Zn(OH)_4]^{2-}]}{[OH^-]^2} = 0.12

The total solubility, SS, of Zn(OH)2Zn(OH)_2 is the sum of the concentrations of all zinc-containing species in solution, excluding the solid Zn(OH)2Zn(OH)_2. In this case, these are Zn2+Zn^{2+} and [Zn(OH)4]2−[Zn(OH)_4]^{2-}.

S=[Zn2+]+[[Zn(OH)4]2−]S = [Zn^{2+}] + [[Zn(OH)_4]^{2-}]

From the first equilibrium, we can express [Zn2+][Zn^{2+}] in terms of [OH−][OH^-]:

[Zn2+]=Ksp[OH−]2[Zn^{2+}] = \frac{K_{sp}}{[OH^-]^2}

From the second equilibrium, we can express [[Zn(OH)4]2−][[Zn(OH)_4]^{2-}] in terms of [OH−][OH^-]:

[[Zn(OH)4]2−]=Kc[OH−]2[[Zn(OH)_4]^{2-}] = K_c [OH^-]^2

Substituting these expressions into the equation for total solubility:

S=Ksp[OH−]2+Kc[OH−]2S = \frac{K_{sp}}{[OH^-]^2} + K_c [OH^-]^2

To find the pH at which the solubility is minimum, we first find the concentration of [OH−][OH^-] at which the solubility SS is minimum. We treat SS as a function of [OH−][OH^-] and find the minimum by taking the derivative with respect to [OH−][OH^-] and setting it to zero. Let x=[OH−]x = [OH^-].

S(x)=Kspx−2+Kcx2S(x) = K_{sp} x^{-2} + K_c x^2

Differentiating S(x)S(x) with respect to xx:

dSdx=−2Kspx−3+2Kcx\frac{dS}{dx} = -2 K_{sp} x^{-3} + 2 K_c x

Set the derivative to zero to find the critical points:

−2Kspx−3+2Kcx=0-2 K_{sp} x^{-3} + 2 K_c x = 0

2Kcx=2Kspx−32 K_c x = 2 K_{sp} x^{-3}

Kcx=Kspx−3K_c x = K_{sp} x^{-3}

Kcx4=KspK_c x^4 = K_{sp}

x4=KspKcx^4 = \frac{K_{sp}}{K_c}

x=(KspKc)1/4x = \left(\frac{K_{sp}}{K_c}\right)^{1/4}

Substitute the given values of KspK_{sp} and KcK_c:

Ksp=1.2×10−17K_{sp} = 1.2 \times 10^{-17}

Kc=0.12=1.2×10−1K_c = 0.12 = 1.2 \times 10^{-1}

[OH−]=(1.2×10−171.2×10−1)1/4[OH^-] = \left(\frac{1.2 \times 10^{-17}}{1.2 \times 10^{-1}}\right)^{1/4}

[OH−]=(10−16)1/4[OH^-] = (10^{-16})^{1/4}

[OH−]=10−4M[OH^-] = 10^{-4} M

This is the concentration of hydroxide ions at which the solubility of Zn(OH)2Zn(OH)_2 is minimum.

Now, we convert this concentration to pOH:

pOH=−log⁡10[OH−]pOH = -\log_{10}[OH^-]

pOH=−log⁡10(10−4)pOH = -\log_{10}(10^{-4})

pOH=4pOH = 4

Finally, we convert pOH to pH using the relationship pH+pOH=14pH + pOH = 14 (at 25∘C25^\circ C):

pH=14−pOHpH = 14 - pOH

pH=14−4pH = 14 - 4

pH=10pH = 10

Thus, the solubility of Zn(OH)2Zn(OH)_2 is minimum at pH 10.