Question

$\qquad z^2 + 4z + 12=0$

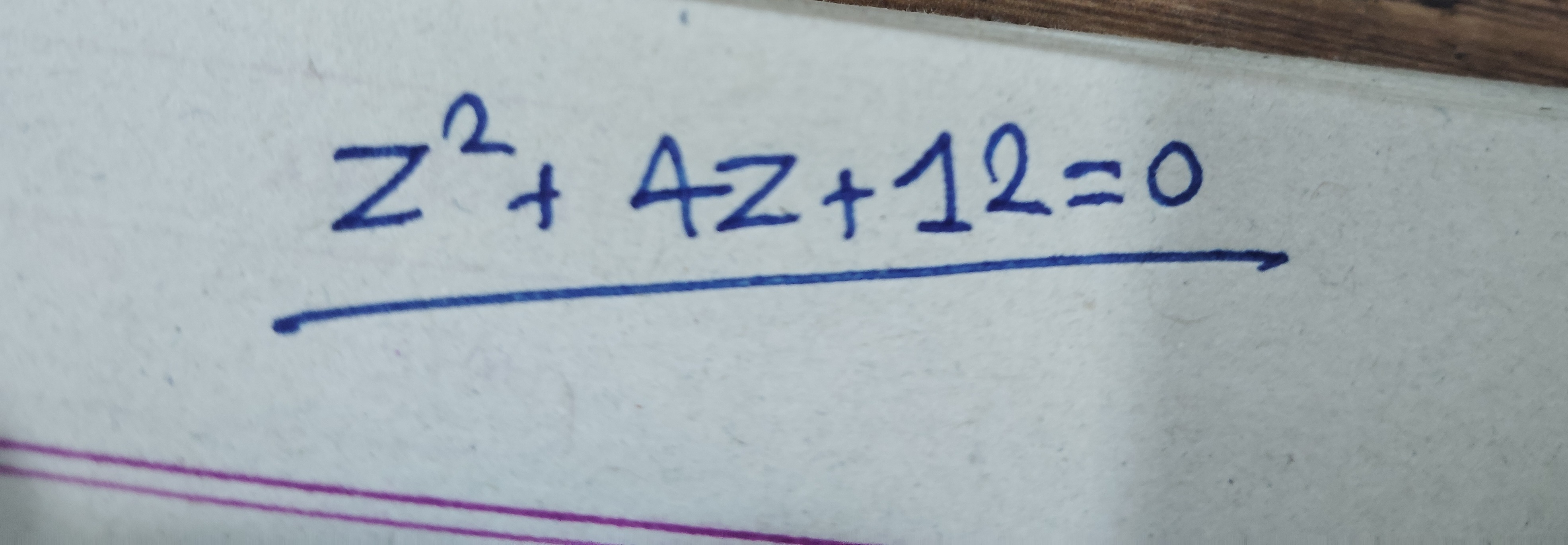
Answer 1

The solutions are $z = -2 + 2\sqrt{2}i$ and $z = -2 - 2\sqrt{2}i$.

Answer 2

The given quadratic equation is $z^2 + 4z + 12 = 0$.
This is in the standard form $az^2 + bz + c = 0$, where $a=1$, $b=4$, and $c=12$.

To solve for $z$, we can use the quadratic formula:

$z = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

First, calculate the discriminant, $D = b^2 - 4ac$:

$D = (4)^2 - 4(1)(12)$
$D = 16 - 48$
$D = -32$

Since the discriminant is negative ($D < 0$), the roots of the equation will be complex numbers.

Now, substitute the values of $a$, $b$, and $D$ into the quadratic formula:

$z = \frac{-4 \pm \sqrt{-32}}{2(1)}$
$z = \frac{-4 \pm \sqrt{32}i}{2}$ (since $\sqrt{-1} = i$)

Simplify $\sqrt{32}$:

$\sqrt{32} = \sqrt{16 \times 2} = \sqrt{16} \times \sqrt{2} = 4\sqrt{2}$

Substitute this back into the expression for $z$:

$z = \frac{-4 \pm 4\sqrt{2}i}{2}$

Now, divide both terms in the numerator by 2:

$z = \frac{-4}{2} \pm \frac{4\sqrt{2}i}{2}$
$z = -2 \pm 2\sqrt{2}i$

Thus, the two solutions for $z$ are:

$z_1 = -2 + 2\sqrt{2}i$
$z_2 = -2 - 2\sqrt{2}i$