Question

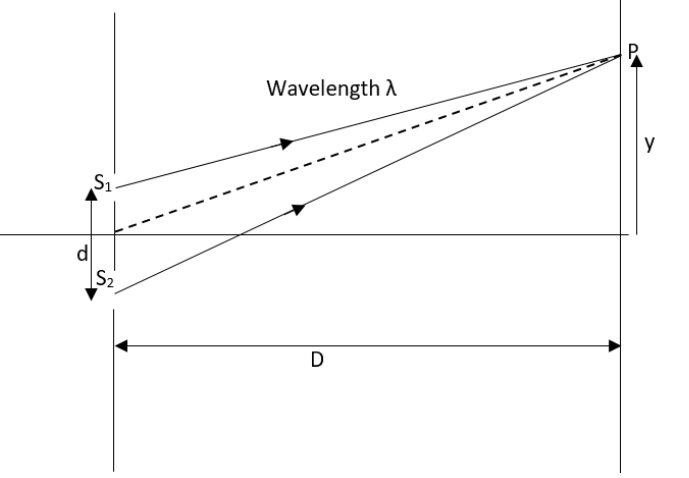
Young's double slit experiment is being carried out using microwaves of wavelength $\lambda =3cm$. Distance between the slits will be $d=5cm$ and the distance between the plane of slits and the screen will be $D=100cm$. Then what will be the number of maximas and their positions on the screen?

Answer 1

The maximum amount of path difference that can be made will be equivalent to the distance between the sources. For the maximum intensity at P, take the difference between ${{S}_{2}}P$ and ${{S}_{1}}P$ which will be equal to the wavelength. This all will help you in answering this question.

Complete step by step answer:
The maximum path difference that can be created will be equivalent to the distance between the sources which has been given as,
$d=5cm$
Therefore as per the conditions mentioned in the question, we will be having only three maximas. That is one central maxima and two on its either side for a path difference of $\lambda$. This has been mentioned as,
$\lambda =3cm$
In order to achieve a maximum intensity at P, the difference between ${{S}_{2}}P$ and ${{S}_{1}}P$ will be equal to the wavelength of the microwaves used.
That is,
${{S}_{2}}P-{{S}_{1}}P=\lambda$…….. (1)
Let us assume that the distance of the maxima from the central fringe is given as $y$. D be the distance between the slit and the screen which has been given as,
$D=100cm$
Let us apply the Pythagoras theorem in the set up.
That is the equation (1) can be written as,
$\sqrt{{{\left( y+\dfrac{d}{2} \right)}^{2}}+{{D}^{2}}}-\sqrt{{{\left( y-\dfrac{d}{2} \right)}^{2}}+{{D}^{2}}}={{\lambda }^{2}}$
Substitute the values in the equation will give,
$\sqrt{{{\left( y+\dfrac{5}{2} \right)}^{2}}+{{100}^{2}}}-\sqrt{{{\left( y-\dfrac{5}{2} \right)}^{2}}+{{100}^{2}}}={{3}^{2}}$
Simplifying this equation will give,

$\Rightarrow y=\pm 75cm$
Therefore the three maximas will be at,
$y=+75cm$
$y=-75cm$
And,
$y=0$

Note: young’s double slit expiring is the demonstration which explains both the particle and wave nature of every particle. It is representing the probabilistic characteristics of quantum mechanical phenomena. This demonstration is exactly similar to electrons as well as for light.