Question

You want to erect a pole of height 10m with the support of three ropes. Each rope has to make an angle of $30{}^\circ$ with the pole. What should be the length of the rope?

Answer 1

Use the fact that in a right-angled triangle the ratio of the adjacent side to the hypotenuse of an angle is equal to cosine of the corresponding angle. Hence prove that $AC=BC\cos 30{}^\circ$. Use the fact that $\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}$ to determine the length of the rope. Verify your answer.

Complete step-by-step answer:

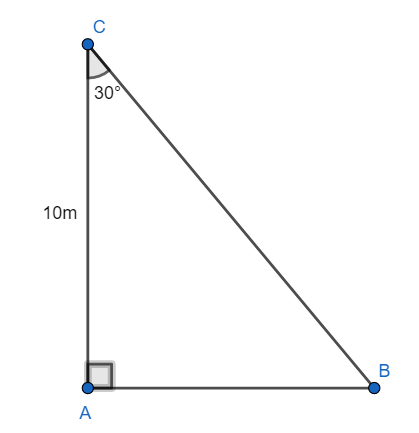
AC is a pole of height 10m. BC is a rope tied to the top of the pole making an angle of $30{}^\circ$ with the pole
To determine: The length BC of the rope
We know that in a right-angled triangle the ratio of the adjacent side to the hypotenuse of an angle is equal to the cosecant of the angle.
In triangle ABC, we have
BC is the hypotenuse and AC is the side adjacent to angle C.
Hence, we have
$\cos C=\dfrac{AC}{BC}$
Multiplying both sides by BC, we get
$AC=BC\cos C$
Since $\angle C=30{}^\circ$, we get
$AC=BC\cos 30{}^\circ$
We know that $\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}$ and AC = 10
Hence, we have
$10=BC\dfrac{\sqrt{3}}{2}$
Multiplying both sides by $\dfrac{2}{\sqrt{3}}$, we get
$BC=\dfrac{20}{\sqrt{3}}$
Hence, the total length of the rope required is $\dfrac{20}{\sqrt{3}}\times 3m=20\sqrt{3}m$

Note: Verification:
We can verify the correctness of our solution by checking that BC = $\dfrac{20}{\sqrt{3}}$ satisfies the condition that $\angle C=30{}^\circ$
We have
$\cos C=\dfrac{AC}{BC}=\dfrac{10}{\dfrac{20}{\sqrt{3}}}=\dfrac{\sqrt{3}}{2}$
We know that $\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}$
Hence, we have
$\begin{aligned} & \cos C=\cos 30{}^\circ \\\ & \Rightarrow C=30{}^\circ \\\ \end{aligned}$
Hence our solution is verified to be correct.