Question

You take two resistors of resistance $2R$ and $3R$ , connect them in parallel in an electric circuit. Calculate the ratio of the electrical power consumed by $2R$ and $3R$ ?

Answer 1

To solve this given question we first start with evaluating the equivalent resistance of the given resistance which are connected in parallel connection. By using the equivalent resistance we will obtain the electrical power by using the relation of power and resistance. Then we will obtain the ratio of the electrical power consumed by the respective resistance given.

Formula used:
Electrical power formula
$P = \dfrac{{{V^2}}}{R}t$
where $V$ is the potential difference and $R$ is resistance and $t$ is the time.

Complete Step-by-step solution
We will consider that the resistance $2R$ and $3R$ connected in parallel and hence the arrangements is given as

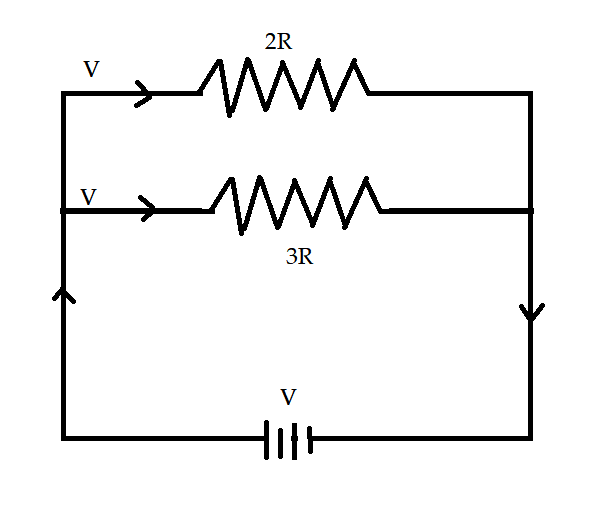
We can conclude from the figure that the resistors are connected in parallel and $V$ are the voltage across the circuit. According to the ohms law that states that for resistance connected in parallel connection the voltage is considered as constant across resistances. Hence from ohm’s law, we can give the formula for electrical power.
Hence from the electrical power formula
$P = \dfrac{{{V^2}}}{R}t$
where $V$ is the potential difference and $R$ is resistance and $t$ is the time.
Hence for the resistance with the value of $2R$ the electrical power is given as
${P_{2R}} = \dfrac{{{V^2}}}{{2R}}t$ ……… $(1)$
Similarly for the resistance with the value of $3R$ the electrical power is given as
${P_{3R}} = \dfrac{{{V^2}}}{{3R}}t$ ……… $(2)$
Now we will evaluate the ratio of electrical power for resistance $2R$ and $3R$ is given by taking the ratio of the equation $(1)$ and $(2)$ ,
$\dfrac{{{P_{2R}}}}{{{P_{3R}}}} = \dfrac{{\dfrac{{{V^2}}}{{2R}}t}}{{\dfrac{{{V^2}}}{{3R}}t}}$
$\Rightarrow \dfrac{{{P_{2R}}}}{{{P_{3R}}}} = \dfrac{{3R}}{{2R}}$
$\therefore \dfrac{{{P_{2R}}}}{{{P_{3R}}}} = \dfrac{3}{2}$
Hence the ratio of the electrical power consumed by $2R$ and $3R$ is given as $\dfrac{{{P_{2R}}}}{{{P_{3R}}}} = \dfrac{3}{2}$ .

Note:
We used the formula of power as $P = \dfrac{{{V^2}}}{R}$ because in the parallel connection voltage across the resistance is found to be constant while for series connection the formula of power can be given by $P = {i^2}Rt$ , where $i$ is current and in series connection current remains constant across the resistances.