Question

You have two resistors of resistance $30\Omega$ and $60\Omega$. What resistances can you get by combining the two?

Answer 1

Firstly, we will connect the resistances in a series combination and calculate the equivalent resistance in this case. Then we will connect the two resistances in a parallel combination and then again we will calculate the equivalent resistance of these two resistors.

Complete step by step solution:
The two basic ways to connect any two resistances are, parallel combination and series combination. In a series combination the starting point of a resistor is the ending point of any other resistor. Whereas in a parallel combination, all the resistances have the same starting point and the ending point.
On connecting the two resistances in series,

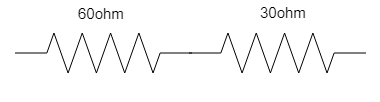
${R_s} = {R_1} + {R_2}$
On putting the value of the two resistors, we get,
${R_s} = 60 + 30$
${R_s} = 90\Omega ......(1)$
So, if we connect the two resistances in a series combination, then the value of the equivalent resistance is ${R_s} = 90\Omega$.
Similarly, if we connect the two resistances in a parallel combination, then,

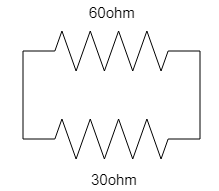
Since, the two resistances are in a parallel combination, so,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
On putting the values of the two resistances, we get,
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{60}} + \dfrac{1}{{30}}$
Now, we will take the LCM,
$\dfrac{1}{{{R_p}}} = \dfrac{{1 + 2}}{{60}}$
$\dfrac{1}{{{R_p}}} = \dfrac{3}{{60}}$
On taking the reciprocal on both the sides, we get,
${R_p} = \dfrac{{60}}{3}$
${R_p} = 20\Omega .......(2)$
So, if we connect the two resistances in a parallel combination, then the value of the equivalent resistance is ${R_p} = 20\Omega$.
So, on connecting the two resistances in series combination, we get the equivalent resistance as ${R_s} = 90\Omega$. On connecting the resistances in parallel, we get the equivalent resistance as ${R_p} = 20\Omega$.

Note:
When two or more resistances are connected in a series combination, then the current flowing through all of them is the same but the potential difference of each of them is different. On the other hand, when two or more resistances are connected in a parallel combination, then the potential difference across each of them is the same but the current in each of them is different.