Question

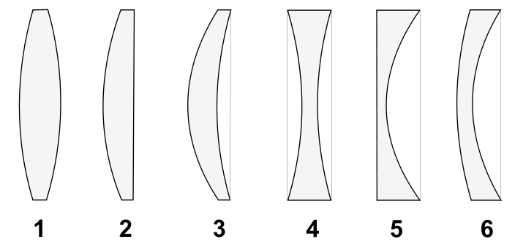
You grind the lenses shown in figure from flat glass disks (n=1.5) using a machine that can grind a radius of curvature of either 40 cm or 60 cm. In a lens where either radius is appropriate, you select the 40 cm radius. Then you hold each lens in the sunshine to form an image of the Sun. What are the (a) focal length f and (b) image type (real or virtual) for (bi-convex) lens 1, (c) f and (d) image type for (plane-convex) lens 2, (e) f and (f) image type for (meniscus convex) lens 3, (g) f and (h) image type for (bi-concave) lens 4, (i) f and (j) image type for (plane-concave) lens 5, and (k) f and (l) image type for (meniscus concave) lens 6?

Answer 1

A lens is a transmissive optical instrument that uses refraction to concentrate or scatter light rays. A simple lens is made up of a single transparent object, while compound lenses are made up of multiple simple lenses aligned around a similar axis. Unlike a prism, which refracts light without concentrating, a lens can concentrate light to form an image.

Complete step by step answer:
The focal length of an optical system is the opposite of the system's optical power; it measures how intensely the system converges or diverges light. A device with a positive focal length converges light, while one with a negative focal length diverges light. A device with a shorter focal range bends the rays more sharply, taking them closer to the focus or diverging them faster.

A biconvex lens is a simple lens that consists of two convex surfaces in a spherical shape, with the same radius of curvature. A convex-convex lens is another name for this kind of lens. The biconvex lens, as a kind of simple lens, has a wide variety of applications, including but not limited to laser beam modulation and focusing, quality photography, and other types of optical instruments. Here, We use the Equation of lens maker with the conventions for signs discussed in Sections.

For lens 1, i.e, the biconvex (or double convex) case, we have
${\text{f}} = {\left[ {({\text{n}} - 1)\left( {\dfrac{1}{{{{\text{r}}_1}}} - \dfrac{1}{{{{\text{r}}_2}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}}= {\left[ {(1.5 - 1)\left( {\dfrac{1}{{40\;{\text{cm}}}} - \dfrac{1}{{ - 40\;{\text{cm}}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}}= 40\;{\text{cm}}$
Here, since focal length is greater than 0 the lens forms a real image of the Sun.

For lens 2, the lens of the planar convex type, we find f
${\text{f}} = {\left[ {({\mathbf{n}} - 1)\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}} = {\left[ {(1.5 - 1)\left( {\dfrac{1}{\infty } - \dfrac{1}{{ - 40\;{\text{cm}}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}} = 80\;{\text{cm}}$
Here, since focal length is greater than 0 the lens forms a real image of the Sun.

Now for lens 3, the lens of the meniscus convex type, we have
${\text{f}} = {\left[ {({\text{n}} - 1)\left( {\dfrac{1}{{{{\text{r}}_1}}} - \dfrac{1}{{{{\text{r}}_2}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}}= {\left[ {(1.5 - 1)\left( {\dfrac{1}{{ - 40}} - \dfrac{1}{{40\;{\text{cm}}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow {\text{f}}= - 40\;{\text{cm}}$

The image formed is virtual since the focal length is lesser than 0.
For lens 5 of the plane-concave type, we have
$f = {\left[ {({\mathbf{n}} - 1)\left( {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow f= {\left[ {(1.5 - 1)\left( {\dfrac{1}{\infty } - \dfrac{1}{{40\;{\text{cm}}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow f= - 80\;{\text{cm}}$
The image formed is virtual since the focal length is lesser than 0. For lens 6 of the meniscus concave type, we have
$f = {\left[ {({\text{n}} - 1)\left( {\dfrac{1}{{{{\text{r}}_1}}} - \dfrac{1}{{{{\text{r}}_2}}}} \right)} \right]^{ - 1}} \\\ \Rightarrow f = {\left[ {(1.5 - 1)\left( {\dfrac{1}{{60\;{\text{cm}}}} - \dfrac{1}{{40\;{\text{cm}}}}} \right)} \right]^{ - 1}} \\\ \therefore f= - 240\;{\text{cm}}$
The image formed is virtual since the focal length is lesser than 0.

Note: After reflection from the mirror, the light rays appear to intersect at a definite point, resulting in a virtual image. A right-side-up photograph is referred to as an upright image. The actual intersection of rays creates an erect image. A set of focus points of light rays coming from an object is known as an image in optics. A composite image is a set of focus points created by extensions of diverging rays, while a real image is a collection of focus points created by converging rays.