Question

You are provided with $8\mu F$ capacitors. Show with help of a diagram how you will arrange the minimum number of them to get a resultant capacitance of $20\mu F$.

Answer 1

Use the formula for the effective capacitance of ‘n’ capacitors when they are connected in series connection and parallel connection. First, try to make the effective capacitance close to $20\mu F$ and then work out for the remaining.

Formula used:
${{C}_{eff}}={{C}_{1}}+{{C}_{2}}$
where ${{C}_{eff}}$ is the effective capacitance of two capacitances ${{C}_{1}}$ and ${{C}_{2}}$ in parallel connection.
${{C}_{eff}}=\dfrac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}}$
where ${{C}_{eff}}$ is the effective capacitance of two capacitances ${{C}_{1}}$ and ${{C}_{2}}$ in series connection.

Complete step by step answer:
To solve the above given question, we will use the formulae for the effective capacitance of ‘n’ capacitors when they are either arranged in a series connection or in a parallel connection.It is said that we are provided with some capacitors with capacitance of $8\mu F$ each and we are supposed to find an arrangement of these capacitors such that the effective capacitance of the arrangement is $20\mu F$.

First, we shall make the effective capacitor close to $20\mu F$ by connecting the capacitors in parallel connection. If we connect two of these capacitors in parallel, then the effective capacitance of the two will be equal to ${{C}_{1}}=8\mu F+8\mu F=16\mu F$. Now, we need another capacitor of $4\mu F$ connected in parallel to these capacitors so that the three capacitances add up to $20\mu F$.

If we connect the two capacitors of capacitance in series, the effective capacitance of the two will be ${{C}_{2}}=\dfrac{8\mu \times 8\mu }{8\mu +8\mu }=4\mu F$
Therefore, we can make a capacitor of $4\mu F$ by connecting two capacitors of $8\mu F$ capacitance in series. With this the final arrangement of these capacitors whose effective capacitance is equal to $20\mu F$ is as shown below.

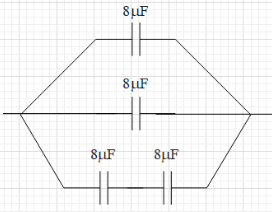
Note: The key thing to know to solve the given problem is that when the capacitors are connected in series, the effective capacitance of the arrangement is greater than each of the capacitances. And when the capacitors are connected in parallel, the effective capacitance of the arrangement is less than each of the capacitances.