Question

You are given several identical resistances each of value $R=10\Omega$ and each capable of carrying a maximum current of one ampere. It is required to make a suitable combination of these resistance of $5\Omega$ which can carry a current of 4 amperes. The minimum number of resistance's of the type R that will be required for this job is
a.) 4
b.) 10
c.) 8
d.) 20

Answer 1

In the given question we need to find out a combination of a circuit which will give the desired output using minimum number of resistors, In such type of questions there is no particular formula to solve. We need to use out thinking power and make a combination in such a way that it satisfies the condition asked in the question.

Complete step by step answer:
In the above question we have been asked to find out the minimum number of resistances required to make a combination of resistance which can carry a current of 4 Amperes and have an equivalent resistance of $5\Omega$
We have been given a condition that we can only use $10\Omega$resistors to make this combination
Now the given quantities are $R=10\Omega$
${{R}_{eq}}=5\Omega$
Now to find the above circuit we have already known that ${{I}_{eq}}=4A$
Now the above combination is only possible when we use 4 segments each of which have two resistors and all the four segments are connected in parallel to each other

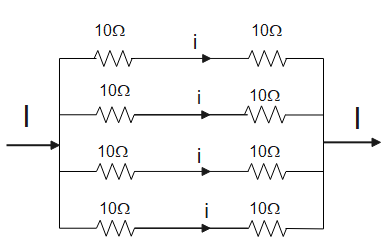
Now if each segment has two resistors this means that each segment has two resistors connected in series and which will make that each segment will have an resistance of $20\Omega$
Now four segments are connected in parallel connection to each other having $20\Omega$ resistance each so the equivalent resistance will be
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}}+\dfrac{1}{{{R}_{4}}}$
Which gives ${{R}_{eq}}=5\Omega$
Now when maximum current flowing through each resistor or we can say that each segment is 1A then the total current in the circuit will be 4A
Therefore, ${{I}_{eq}}=4A$
Hence, we can say that minimum 8 number of resistances is required make this circuit

So, the correct answer is “Option c”.

Note: The value of current remains same in a series circuit and hence in this way each of the segment have two resistor and each of the resistor have equal amount of current, that is 1 Ampere because they are connected in series to each other in the given segment and we have 4 segments that give us the total current of 4 Ampere.