Solveeit Logo
Login

Question

Question: You are given \(n\) identical resistors each of resistance \(r\Omega \). First they are connected in...

You are given nn identical resistors each of resistance rΩr\Omega . First they are connected in such a way that the possible minimum value of resistance is gained. Then they are connected in a way to get a maximum possible resistance. The ratio of the minimum and maximum resistance gained in these ways is given as _____.
A.1n B.n C.n2 D.1n2 \begin{aligned} & A.\dfrac{1}{n} \\\ & B.n \\\ & C.{{n}^{2}} \\\ & D.\dfrac{1}{{{n}^{2}}} \\\ \end{aligned}

Explanation

Solution

When the resistance is connected in a series connection, then the total resistance is given as the product of the number of resistors connected and the resistance of a resistor. When the resistance is connected in a parallel connection, then the resistance is given as the product of the value of resistance and the reciprocal of the number of resistors connected.

Complete answer:
It is mentioned in the question that,
Number of resistors used is given as nn.
The value of the resistance is given as the value mentioned as rr.
Therefore the total resistance of the circuit which is connected in series will be the product of the resistance of the resistor and number of resistors. This can be written as,
RS=nr{{R}_{S}}=nr
This resistance will be the maximum resistance of the circuit.

Now the total resistance of the circuit when it is connected parallel will be given as the product of the value of resistance and the reciprocal of the number of resistors connected.

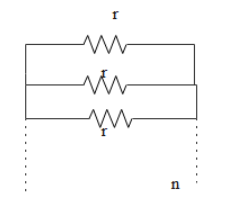
Therefore the total resistance can be written as,
RP=r×1n{{R}_{P}}=r\times \dfrac{1}{n}
This will be the minimum resistance possible. Therefore the ratio of the minimum and the maximum resistance obtained will be,
minimum resistancemaximum resistance=r×1nnr=1n2\dfrac{\text{minimum resistance}}{\text{maximum resistance}}=\dfrac{r\times \dfrac{1}{n}}{nr}=\dfrac{1}{{{n}^{2}}}

Therefore the answer for this question has been obtained which is given as the option D.

Note:
The parallel connected components will be connected along multiple paths so that the current will be divided and the same voltage will be the same. In series connection, the current will be the same in full circuit. The voltage will be divided according to the components connected.