Question

You are given marbles of diameter 10 mm. They are to be placed such that their centers are laying in a square-bound by four lines each of length 40 mm. What will be the arrangements of marbles in a plane so that the maximum number of marbles can be placed inside the area? Sketch the diagram, and derive an expression for the number of molecules per unit area.

Answer 1

To derive the number of molecules per unit area, draw the diagram in a square you can place the marbles giving a spherical shape. The spheres are arranged in the ABAB manner such that the rectangle formed by joining the centers of the sphere is an equilateral triangle. The triangle has each angle equal to $\text{ 6}{{\text{0}}^{\text{0}}}\text{ }$ . The side of the triangle can be calculated by the sine. It is given as,
$\text{ }\sin \theta \text{ = }\dfrac{\text{side}}{\text{hypotenuse}}\text{ }$

Complete step by step answer:
Firstly, let us sketch a diagram accordingly,


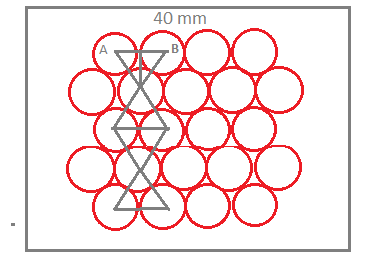
- In the figure, we have represented the side of the square by 40 mm as given in the question, and the marbles are placed in it.
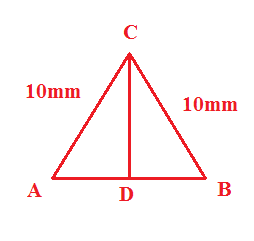
-Now, firstly, we will calculate the CD. The CD can be calculated by the trigonometric relation between the AD, AC, and the AD. The angle of sine is given as,
$\text{ }\sin \theta \text{ = }\dfrac{\text{side}}{\text{hypotenuse}}\text{ = }\dfrac{\text{CD}}{\text{AC}}\text{ }$
Since it is an equilateral triangle thus each angle in the triangle is equal to$\text{ 6}{{\text{0}}^{\text{0}}}\text{ }$. Thus the value of CD is equal to,
$\begin{aligned} & \sin {{60}^{0}}\text{ = }\dfrac{\text{CD}}{\text{AC}}\text{ = }\dfrac{\text{CD}}{\text{10}} \\\ & \Rightarrow \text{CD = 10}\sin {{60}^{0}}\text{ = 10 }\times \dfrac{\sqrt{3}}{2}\text{ = 5}\sqrt{3}\text{ } \\\ \end{aligned}$
We can calculate the area of a square consisting of spherical marbles. The area of the square is equal to the square of the side. The area of the square is,
$\text{ Area of square = (side}{{\text{)}}^{\text{2}}}\text{ }$
Therefore, the area of the marble is given as,
$\text{ Area of square marble = 40 }\times \text{ 40 = 1600 m}{{\text{m}}^{\text{2}}}\text{ =16 c}{{\text{m}}^{\text{2}}}\text{ }$
-Now, from the diagram, we can see the maximum number of spheres of diameter $\text{ 10 mm }$ represented in hcp packing.
-Thus, we can calculate the total length covered by spheres in the square. Thus the total length covered by the square in the square is calculated as,
$\text{ Total length = 5 + 4 }\times \text{10 sin 6}{{\text{0}}^{\text{0}}}\text{ = 5 + 4 }\times \text{10 }\times \dfrac{\sqrt{3}}{2}\text{ = 39}\text{.2 mm }\simeq \text{ 40 mm }$
The millimeter can be expressed as the centimeter .the relation between the millimeter and centimeter is,$\text{ 10 mm = 1cm }$
Thus,
$\text{ 40 mm = }\dfrac{\text{40 m}}{10\text{ m}}\text{ }\times \text{ 1cm = 4 cm }$
- Further, calculate the maximum number of spheres would be equal to the sum of the full 14 spheres and the 8 half spheres. The maximum number of the sphere is,
$\text{ Max}\text{.no of spheres = 1 }\times \text{ 14 + }\dfrac{1}{2}\text{ }\times \text{ 8 = 18 }$
-Thus, the number of spheres per $\text{ c}{{\text{m}}^{\text{2}}}\text{ }$ of the square is equal to the,
$\text{ No}\text{. of sphere per c}{{\text{m}}^{\text{2}}}\text{ of square = }\dfrac{\text{Total no}\text{.of sphere}}{\text{Area of square }}\text{ = }\dfrac{18}{16}\text{ = 1}\text{.125 c}{{\text{m}}^{-\text{2}}}\text{ }$

-In the last, we can conclude that the number of molecules per unit area is $\text{ 1}\text{.125 c}{{\text{m}}^{-\text{2}}}\text{ }$

Note: The above sketch suggests that hcp (hexagonal close packing) exists with the maximum number of spheres in the figure. Packing efficiency is the space occupied by spherical atoms in the crystal lattice. The packing efficiency of hcp lattice is generally $\text{ 74}{\scriptstyle{}^{0}/{}_{0}}\text{ }$. It is calculated by considering the ratio of volume occupied by the number of atoms in the structure to the total volume of the structure.