Question
Question: $y=\frac{(e^{sinx}-1)^4+((cosx-1)e^{sinx})^3+(e^x+e^{-x})^3+x^3+2x^2+4}{e^x}$ $y''(0)=?$...
y=ex(esinx−1)4+((cosx−1)esinx)3+(ex+e−x)3+x3+2x2+4
y′′(0)=?
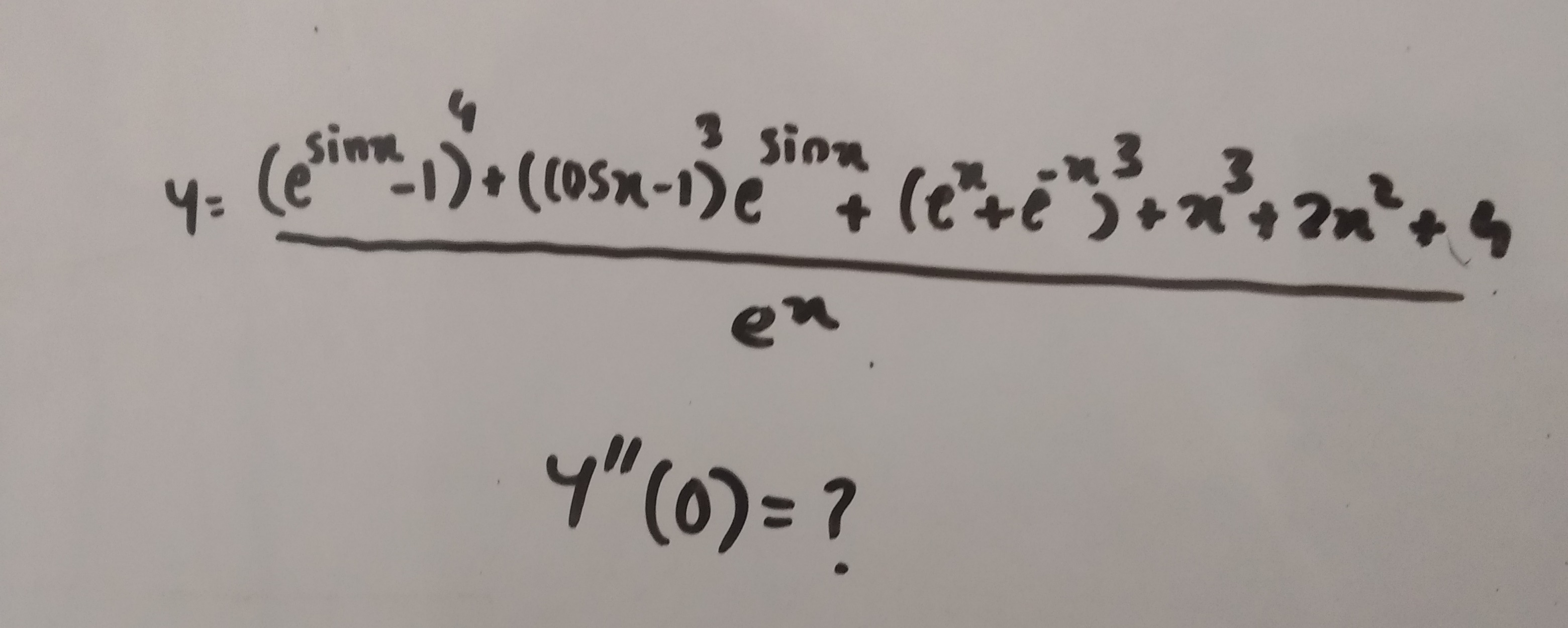
40
Solution
The function is given by y(x)=ex(esinx−1)4+((cosx−1)esinx)3+(ex+e−x)3+x3+2x2+4.
Let the numerator be N(x)=(esinx−1)4+((cosx−1)esinx)3+(ex+e−x)3+x3+2x2+4. Then y(x)=N(x)e−x.
To find y′′(0), we first find the derivatives of y(x): y′(x)=N′(x)e−x−N(x)e−x=(N′(x)−N(x))e−x y′′(x)=(N′′(x)−N′(x))e−x−(N′(x)−N(x))e−x=(N′′(x)−2N′(x)+N(x))e−x At x=0, y′′(0)=(N′′(0)−2N′(0)+N(0))e−0=N′′(0)−2N′(0)+N(0).
Let's evaluate N(0), N′(0), and N′′(0). N(x)=(esinx−1)4+((cosx−1)esinx)3+(ex+e−x)3+x3+2x2+4 At x=0: sin0=0, cos0=1. N(0)=(e0−1)4+((1−1)e0)3+(e0+e−0)3+03+2(0)2+4 N(0)=(1−1)4+(0⋅1)3+(1+1)3+0+0+4 N(0)=04+03+23+4=0+0+8+4=12.
To find N′(0) and N′′(0), we can use Taylor series expansions of the terms around x=0. Recall the series expansions: sinx=x−6x3+O(x5) cosx=1−2x2+24x4+O(x6) eu=1+u+2u2+6u3+24u4+...
Term 1: T1=(esinx−1)4 esinx=1+sinx+2sin2x+6sin3x+24sin4x+O(x5) =1+(x−6x3)+2(x−6x3)2+6(x)3+24(x)4+O(x5) =1+x−6x3+2x2−x4/3+O(x6)+6x3+24x4+O(x5) =1+x+2x2+x3(−61+61)+x4(−61+241)+O(x5) =1+x+2x2−8x4+O(x5) esinx−1=x+2x2−8x4+O(x5) T1=(esinx−1)4=(x+2x2−8x4+O(x5))4=x4+4x3(2x2)+O(x6)=x4+2x5+O(x6). T1(x)=c4x4+c5x5+... T1′(x)=4c4x3+5c5x4+...⟹T1′(0)=0. T1′′(x)=12c4x2+20c5x3+...⟹T1′′(0)=0.
Term 2: T2=((cosx−1)esinx)3 cosx−1=−2x2+24x4+O(x6) esinx=1+x+2x2+O(x3) (cosx−1)esinx=(−2x2+O(x4))(1+x+O(x2))=−2x2−2x3+O(x4). T2=((cosx−1)esinx)3=(−2x2−2x3+O(x4))3=(−2x2)3+3(−2x2)2(−2x3)+O(x8) =−8x6−83x7+O(x8). T2(x)=d6x6+d7x7+... T2′(x)=6d6x5+7d7x6+...⟹T2′(0)=0. T2′′(x)=30d6x4+42d7x5+...⟹T2′′(0)=0.
Term 3: T3=(ex+e−x)3 ex=1+x+2x2+6x3+24x4+O(x5) e−x=1−x+2x2−6x3+24x4+O(x5) ex+e−x=2+x2+12x4+O(x6) T3=(2+x2+12x4+O(x6))3 =23+3⋅22(x2+12x4+O(x6))+3⋅2(x2+O(x4))2+(x2+O(x4))3 =8+12(x2+12x4+O(x6))+6(x4+O(x6))+O(x6) =8+12x2+x4+6x4+O(x6)=8+12x2+7x4+O(x6). T3(x)=8+12x2+7x4+... T3′(x)=24x+28x3+...⟹T3′(0)=0. T3′′(x)=24+84x2+...⟹T3′′(0)=24.
Term 4: T4=x3+2x2+4 T4′(x)=3x2+4x⟹T4′(0)=0. T4′′(x)=6x+4⟹T4′′(0)=4.
N(x)=T1+T2+T3+T4. N′(x)=T1′+T2′+T3′+T4′. N′(0)=T1′(0)+T2′(0)+T3′(0)+T4′(0)=0+0+0+0=0.
N′′(x)=T1′′+T2′′+T3′′+T4′′. N′′(0)=T1′′(0)+T2′′(0)+T3′′(0)+T4′′(0)=0+0+24+4=28.
Finally, y′′(0)=N′′(0)−2N′(0)+N(0). y′′(0)=28−2(0)+12=28+12=40.
The final answer is 40.
Explanation of the solution:
- Define the numerator of the function as N(x) and write y(x)=N(x)e−x.
- Calculate the second derivative y′′(x) using the product rule. Evaluate y′′(0) in terms of N(0), N′(0), and N′′(0).
- Evaluate N(0) by substituting x=0 into the expression for N(x).
- Evaluate N′(0) and N′′(0) by finding the first and second derivatives of each term in N(x) and evaluating them at x=0. Taylor series expansions around x=0 are used to efficiently determine the values of the derivatives at x=0. For terms starting with powers of x greater than 1, the first and second derivatives at x=0 are zero.
- Substitute the calculated values of N(0), N′(0), and N′′(0) into the expression for y′′(0).
The final answer is 40.
