Solveeit Logo
Login

Question

Question: Yellow light (\[\lambda \] = 6000 A°) illuminates a single slit of width \(1 \times {10^{ - 4}}\) m....

Yellow light (λ\lambda = 6000 A°) illuminates a single slit of width 1×10−41 \times {10^{ - 4}} m. Calculate the distance between two dark lines on either side of the central maximum when the diffraction pattern is viewed on a screen kept 1.5 m away from the slit.

Explanation

Solution

The wavelength of the light, the width of the slit and the distance is given, using which we can find out the angular separation of the bands and hence the actual distance. The actual distance between the bands can be obtained from the relation between angular separation and actual distance.

Complete step by step solution:
The wavelength of the given yellow light is 6000 A, which is 6000×10−106000 \times {10^{ - 10}} m. The width of the slit is represented as d, which is 1×10−41 \times {10^{ - 4}} m. The distance between the slit and the screen is 1.5 m, represented as L.

The light is passed through a single slit, so we see a diffraction pattern forms on the screen. There is a central maxima which is the brightest. Then, on either side of the maxima, there is a dark band followed by a bright band. This pattern continues on the screen. However, the brightness of all the bands is not the same in case of diffraction. As we move away from the central maxima, the brightness reduces. The central maxima is the brightest on the screen.


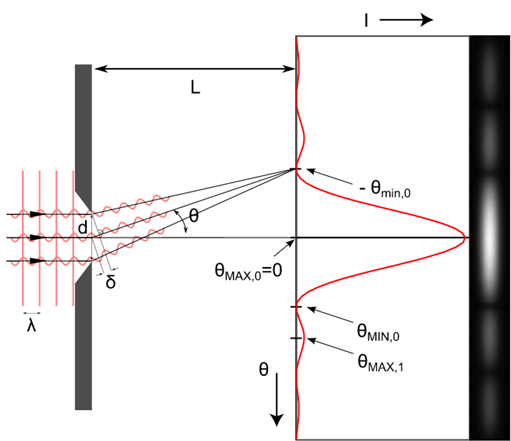
The angular separation of the dark bands on each side of the central bright band is given by,
2θ=2λd2\theta = \dfrac{{2\lambda }}{d} …equation (1)
In equation (1), we multiply by 2 because we need to find out the separation between bands on either side of the central bright band. On substituting the values of the term on the right side of the equation, we obtain,
Angular separation, 2θ=2×6000×10−101×10−4=1.2×10−22\theta = \dfrac{{2 \times 6000 \times {{10}^{ - 10}}}}{{1 \times {{10}^{ - 4}}}} = 1.2 \times {10^{ - 2}}

But, we need the actual separation of the two dark bands. So, we multiply the angular separation obtained with the distance between the slot and the screen. We obtain,
Actual distance, 2x=2θ×L=2λd×L2x = 2\theta \times L = \dfrac{{2\lambda }}{d} \times L
On substituting the values on the right hand side of the above equation, we get,
Actual distance, 2x=1.2×10−2×1.5=1.8×10−22x = 1.2 \times {10^{ - 2}} \times 1.5 = 1.8 \times {10^{ - 2}} m

Hence, the distance between two dark bands on either side of the central bright band is 1.8×10−21.8 \times {10^{ - 2}} m or 18 mm.

Note: This formula cannot be used when two slits are present. The case of two slits, which represents interference, is governed by the Young’s double slit experiment. Interference and diffraction are different phenomena.