Question

$y=4^{\log_2 \sin x + 9^{\log_3 \cos x}}$

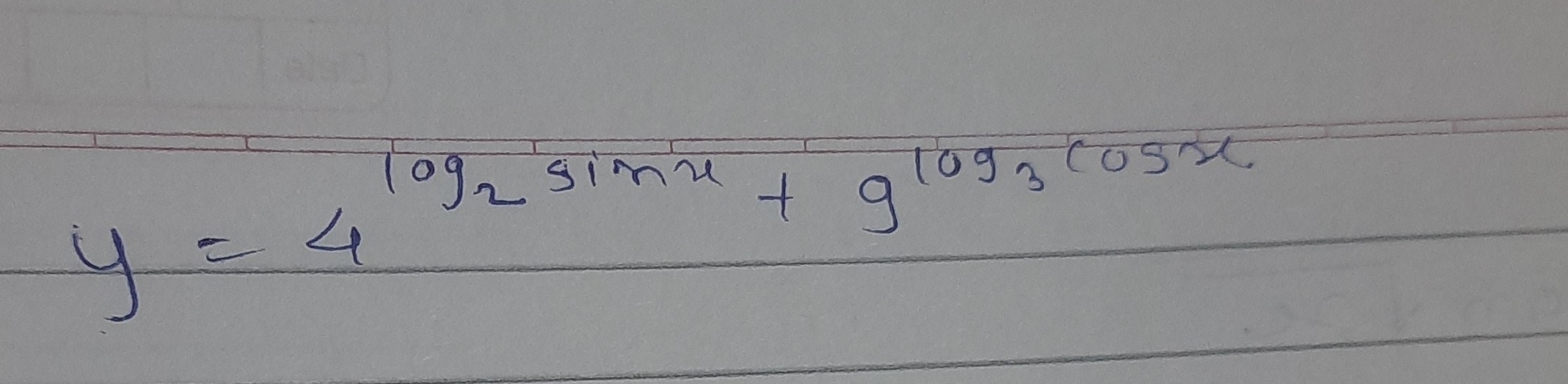
Answer 1

$\frac{dy}{dx}=2\sin x\cos x\cdot 4^{\cos^2 x}\Bigl[1- (\sin x)^2\ln 4\Bigr]$.

Answer 2

We start with

$$y=4^{\log_2 \sin x+9^{\log_3 \cos x}}.$$

Using the property $a^{u+v}=a^u\cdot a^v$ we write

$$y=4^{\log_2 \sin x}\cdot 4^{9^{\log_3 \cos x}}.$$

1. For the first factor, use the identity
     $a^{\log_b c} = c^{\log_b a}$:
     $4^{\log_2 \sin x} = (\sin x)^{\log_2 4}=(\sin x)^2,$   since $\log_2 4=2$.

2. For the second factor, first simplify the exponent
     $9^{\log_3 \cos x}=(\cos x)^{\log_3 9}=(\cos x)^2,$   since $\log_3 9=2$. Then,   $4^{9^{\log_3 \cos x}}= 4^{(\cos x)^2}.$

Thus,

$$y=(\sin x)^2\cdot 4^{\cos^2 x}.$$

Write $4^{\cos^2 x}=e^{\cos^2 x\ln 4}$. Now differentiate using the product rule:

Let

$$u=\sin^2 x,\quad u' =2\sin x\cos x,$$ $$v=4^{\cos^2 x}=e^{\cos^2 x\ln 4},\quad \text{so}\quad v'=4^{\cos^2 x}\ln 4\cdot \frac{d}{dx}(\cos^2 x).$$

Differentiate $\cos^2 x$ using the chain rule:

$$\frac{d}{dx}(\cos^2 x)=-2\cos x\sin x.$$

Thus,

$$v'=-2\ln 4\sin x\cos x\cdot 4^{\cos^2 x}.$$

Applying the product rule:

$$\frac{dy}{dx}= u'v+uv' = \bigl[2\sin x\cos x\cdot 4^{\cos^2 x}\bigr] + \bigl[(\sin x)^2\cdot (-2\ln 4\sin x\cos x\cdot 4^{\cos^2 x})\bigr].$$

Factor common terms $2\sin x\cos x\cdot 4^{\cos^2 x}$:

$$\frac{dy}{dx}=2\sin x\cos x\cdot 4^{\cos^2 x}\Bigl[1- (\sin x)^2\ln 4\Bigr].$$