Question

y = tan^{-1}(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}})

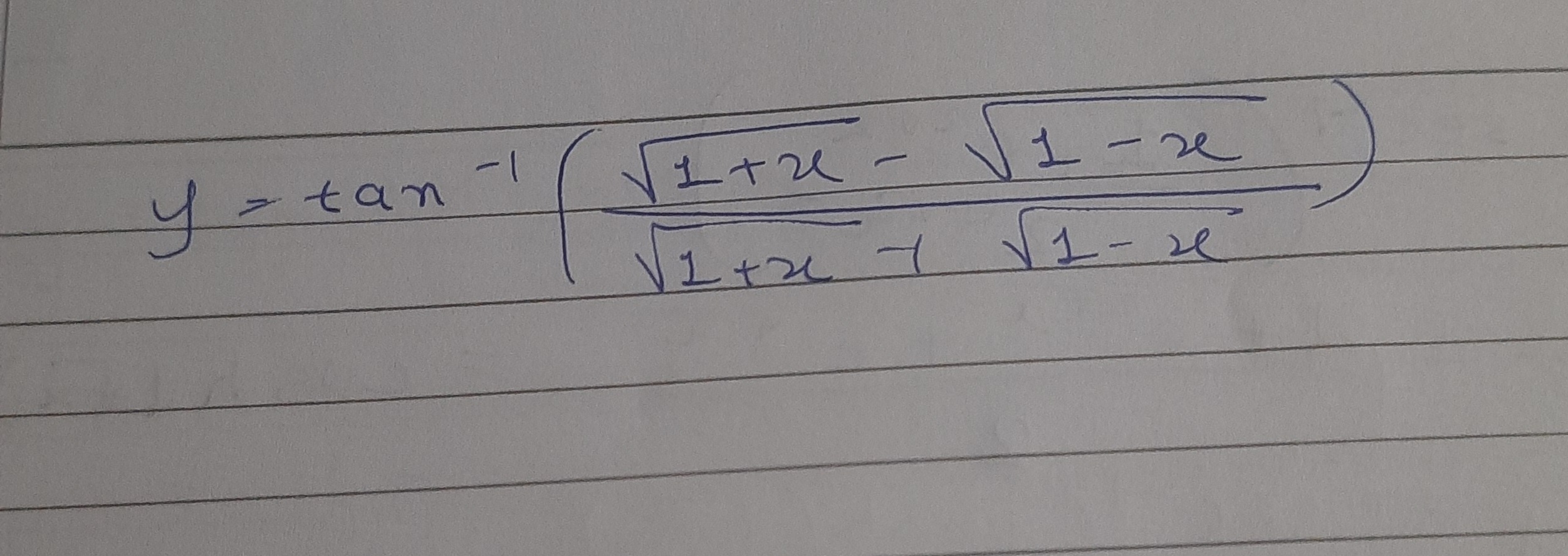
Answer 1

\frac{dy}{dx}=0.

Answer 2

Solution:

We are given

$$y=\tan^{-1}\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}\right).$$

Since the numerator and denominator are identical (except when they vanish),

$$\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}} = 1 \quad \text{for } x \neq 0.$$

Thus,

$$y=\tan^{-1}(1)=\frac{\pi}{4},$$

which is a constant.

Differentiating a constant, we get

$$\frac{dy}{dx}=0.$$

Quick Explanation:

• Simplify the fraction to 1.
• $y=\tan^{-1}(1)=\pi/4$ is constant, so its derivative is 0.