Question
Question: $y = \sqrt[3]{\tan x}$ $\qquad x$...
y=3tanx x
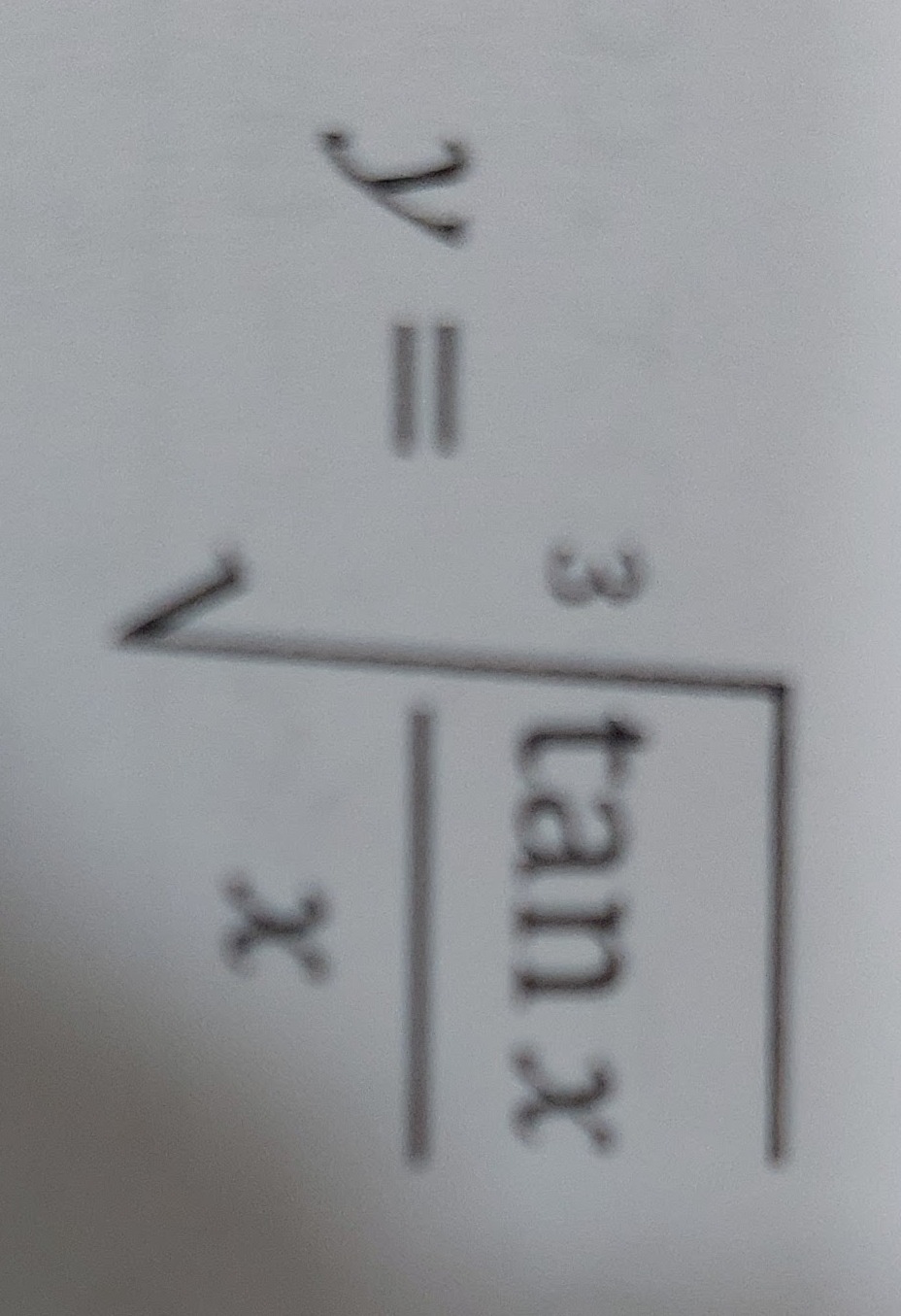
Answer
The domain of the function is
{x∈R:x=0 and x=2π+kπ,k∈Z}.Explanation
Solution
Explanation:
For the function
the cube root is defined for all real numbers. Thus, restrictions come from the expression inside the cube root:
- The denominator x must not be zero (i.e. x=0).
- tanx is undefined when cosx=0; that is, for x=2π+kπ where k∈Z.
Answer:
The domain of the function is
