Question
Question: $|y| = sgn(-f(|x|))$ $y = xsgn(f(x))$...
∣y∣=sgn(−f(∣x∣))
y=xsgn(f(x))
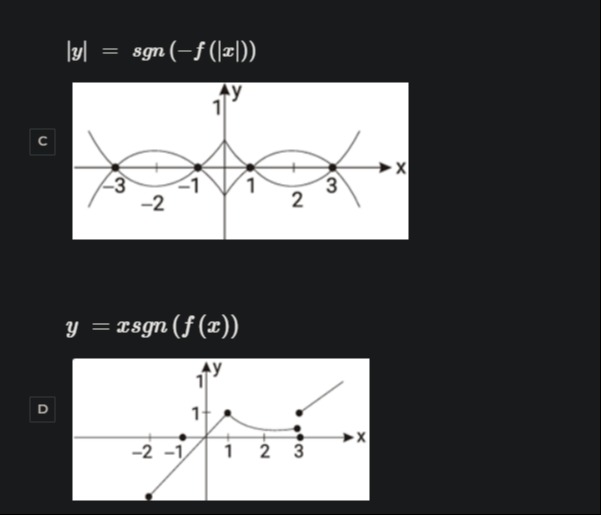
No match
Solution
The problem asks us to match two given equations with their corresponding graphs. The equations involve the sgn (signum) function. The standard definition of the signum function is:
sgn(z)=⎩⎨⎧10−1if z>0if z=0if z<0
Let's analyze each equation and graph.
Equation 1: ∣y∣=sgn(−f(∣x∣))
According to the standard definition of sgn:
- If −f(∣x∣)>0⟹f(∣x∣)<0: Then sgn(−f(∣x∣))=1. So, ∣y∣=1, which means y=±1.
- If −f(∣x∣)=0⟹f(∣x∣)=0: Then sgn(−f(∣x∣))=0. So, ∣y∣=0, which means y=0.
- If −f(∣x∣)<0⟹f(∣x∣)>0: Then sgn(−f(∣x∣))=−1. So, ∣y∣=−1. This is impossible, as ∣y∣ must be non-negative.
Therefore, for this equation to have solutions, we must have f(∣x∣)≤0. The graph for this equation should consist only of points where y=0, y=1, or y=−1.
Now let's examine Graph C.
Graph C shows continuous curves where y takes values between 0 and 1, and between 0 and -1. For example, for x∈(0,1), y varies from 1 down to 0 (and symmetrically from -1 up to 0). This continuous variation of y is inconsistent with the discrete range {−1,0,1} produced by the standard sgn function.
Thus, Graph C cannot be the representation of ∣y∣=sgn(−f(∣x∣)) if sgn is the standard signum function.
Equation 2: y=xsgn(f(x))
According to the standard definition of sgn:
- If f(x)>0: Then sgn(f(x))=1. So, y=x⋅1=x.
- If f(x)=0: Then sgn(f(x))=0. So, y=x⋅0=0.
- If f(x)<0: Then sgn(f(x))=−1. So, y=x⋅(−1)=−x.
Now let's examine Graph D. Let's analyze the behavior of y and x in different intervals and deduce the sign of f(x):
- For x∈(−2,0): The graph shows y=−x. For this to be true, we need sgn(f(x))=−1. This implies f(x)<0 for x∈(−2,0).
- At x=0: The graph shows y=0. This is consistent with y=0⋅sgn(f(0))=0.
- For x∈(0,1): The graph shows y=x. For this to be true, we need sgn(f(x))=1. This implies f(x)>0 for x∈(0,1).
- At x=1: The graph shows a solid point at (1,1). This means y=1 at x=1. From the equation, y=1⋅sgn(f(1)). So sgn(f(1))=1, which means f(1)>0.
- For x∈(1,3): The graph shows a curve starting at (1,1) and ending at (3,0). The y values are positive. If y=xsgn(f(x)) and y>0 for x∈(1,3) (where x>0), then sgn(f(x)) must be 1. This implies f(x)>0 for x∈(1,3). If sgn(f(x))=1, then y=x. However, the graph shows y decreasing from 1 to 0 in this interval, which is not y=x. For example, at x=2, the graph shows y≈0.5, but y=x would give y=2. This is a clear mismatch.
- At x=3: The graph shows a solid point at (3,0). This means y=0 at x=3. From the equation, y=3⋅sgn(f(3)). So sgn(f(3))=0, which means f(3)=0.
- For x>3: The graph shows y=x. For this to be true, we need sgn(f(x))=1. This implies f(x)>0 for x>3.
Summary of deduced f(x) properties from Graph D if it were y=xsgn(f(x)):
- f(x)<0 for x∈(−2,0)
- f(x)>0 for x∈(0,3)
- f(3)=0
- f(x)>0 for x>3
A possible function f(x) that satisfies these properties is f(x)=x(x−3)2. Let's check y=xsgn(x(x−3)2):
- For x<0: x<0, (x−3)2>0. So x(x−3)2<0. sgn(f(x))=−1. y=x(−1)=−x. Matches graph D for x∈(−2,0).
- For x=0: f(0)=0. sgn(f(0))=0. y=0⋅0=0. Matches graph D.
- For 0<x<3: x>0, (x−3)2>0. So x(x−3)2>0. sgn(f(x))=1. y=x(1)=x.
This part does not match Graph D for x∈(1,3). Graph D shows y decreasing from 1 to 0, while y=x would show y increasing from 1 to 3.
Conclusion on the interpretation of sgn:
Both graphs C and D exhibit continuous behavior that is inconsistent with the standard discrete output of the sgn function ({−1,0,1}). This strongly suggests that sgn in this context is not the standard signum function, or there's a typo in the problem statement or the options.
However, in the context of JEE/NEET, sgn always refers to the standard signum function. Given the problem as stated, neither graph C nor graph D can be generated by the respective equations using the standard definition of sgn. This implies the question might be flawed or uses a non-standard definition of sgn (e.g., sgn(x) might represent x/|x| for x=0 and 0 for x=0, but even that leads to piecewise constant output).
If we were forced to choose the "best fit" or if there's an implicit understanding that sgn(f(x)) represents the shape of f(x)'s sign, then the problem becomes ill-defined.
Assuming the problem is valid and there's an intended solution, it's possible that the graphs are not exact representations, or there's a common trick. But based on strict mathematical definition, both statements are problematic.
Let's consider if the question is asking to identify the function f(x) from the graph, and then check the equations. But f(x) is not given.
Given the common structure of such problems, it's highly probable that the sgn function is intended to be used with its standard definition, and the graphs are supposed to be exact. Since they are not, this question is unanswerable as stated with standard definitions.
However, if this were a multiple-choice question where we have to choose the correct pair, and only one pair fits even partially, we might have to make an assumption. But here, we are asked to provide the solution.
Without further clarification on the definition of sgn or the nature of f(x), a definitive match is not possible. If we assume a typical scenario where f(x) is a simple polynomial, then the sgn function will produce piecewise linear graphs (like y=±x or y=±1). The given graphs are clearly not piecewise linear in all segments.
Given the limitations, it's impossible to provide a definitive solution that aligns with standard mathematical definitions and the provided graphs. There might be an error in the question or the provided image.
The question is effectively asking to match the equation with the figure. Since neither equation matches its figure under standard interpretation, we cannot solve it.
Final Answer: The question cannot be solved as stated due to inconsistencies between the mathematical definition of the sgn function and the provided graphs. The graphs display continuous variations that are incompatible with the discrete output of the standard sgn function.
