Question
Question: $\displaystyle y = sec^{-1}(\frac{1+e^{2\sqrt{x}}}{2e^{\sqrt{x}}})$...
y=sec−1(2ex1+e2x)
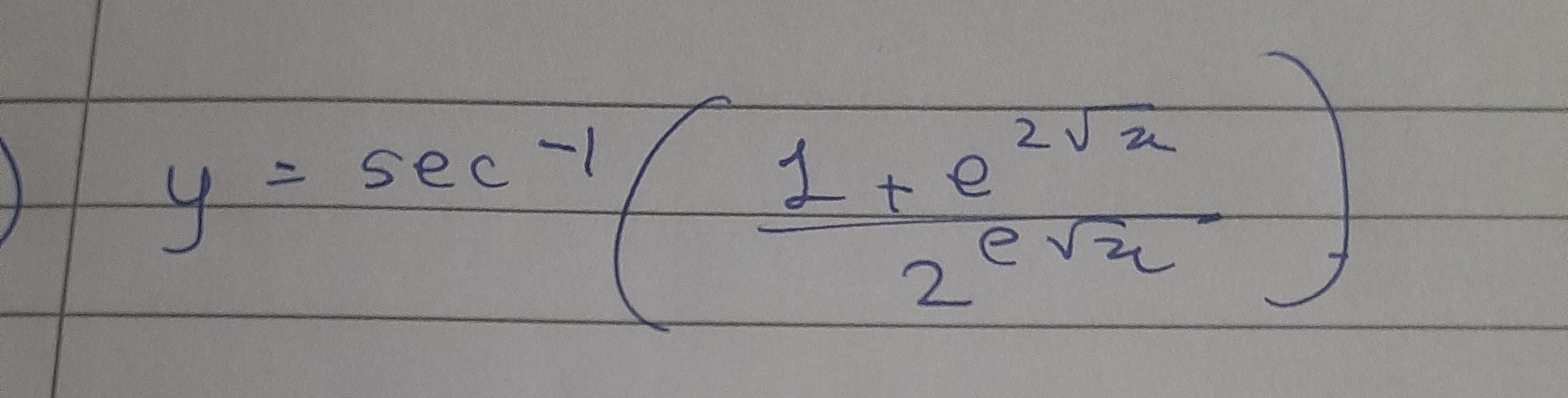
Answer
dxdy=2xcoshx1
Explanation
Solution
We start with
y=sec−1(2ex1+e2x).Notice that
2ex1+e2x=2ex+e−x=coshx.Thus,
y=sec−1(coshx).The derivative formula for y=sec−1(u) (with u>0) is
dxdy=uu2−1u′(x).Here, u(x)=coshx. Differentiate using the chain rule:
u′(x)=dxdcoshx=sinhx⋅2x1=2xsinhx.Since
u2−1=cosh2x−1=sinh2x=sinhx(for x>0),we have
dxdy=coshxsinhx2xsinhx=2xcoshx1.