Question

$y \log y \, dx + (x - \log y)dy = 0$

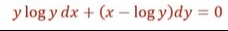
Answer 1

x \log y = \frac{(\log y)^2}{2} + C

Answer 2

The given differential equation $y \log y \, dx + (x - \log y)dy = 0$ is a first-order differential equation. It can be transformed into a linear differential equation in $x$ with $y$ as the independent variable.

1. Rearrange the equation: $\frac{dx}{dy} + \frac{1}{y \log y} x = \frac{1}{y}$.

2. Identify $P(y) = \frac{1}{y \log y}$ and $Q(y) = \frac{1}{y}$.

3. Calculate the integrating factor (IF): $e^{\int P(y) dy} = e^{\int \frac{1}{y \log y} dy} = e^{\log|\log y|} = \log y$.

4. Apply the general solution formula for linear equations: $x \cdot (\text{IF}) = \int Q(y) \cdot (\text{IF}) \, dy + C$.

5. Substitute and integrate: $x \log y = \int \frac{1}{y} \log y \, dy + C = \frac{(\log y)^2}{2} + C$.

The final solution is $x \log y = \frac{(\log y)^2}{2} + C$.