Question

y = f (x) is a parabola having directrix with slope 0. If $f^2(0) + f^2(1) + f^2(2) + 45 = 10f(0) + 8f(1) + 4f(2)$, then -

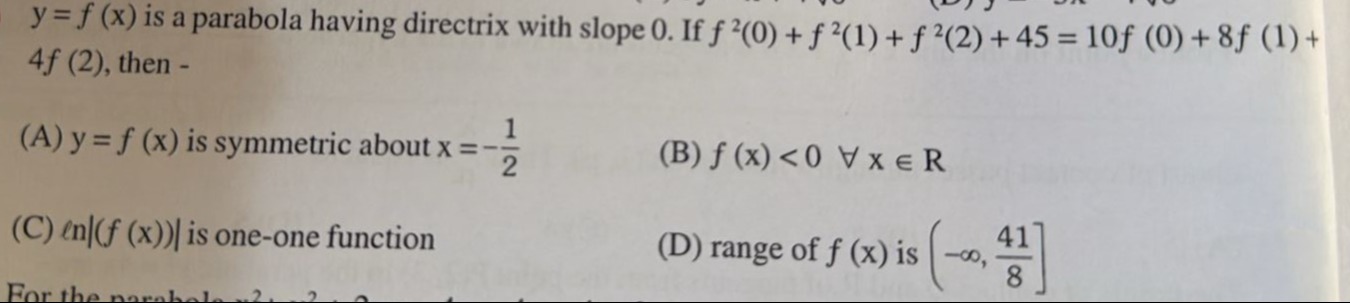
• A. y = f (x) is symmetric about x = $-\frac{1}{2}$
• B. f (x) <0 ∀x∈R
• C. $\ln|(f (x))|$ is one-one function
• D. range of f (x) is $(-\infty,\frac{41}{8}]$

Answer 1

Answer: (A), (D)

(A), (D)

Answer 2

The given equation $y = f(x)$ represents a parabola whose directrix has a slope of 0. This implies the directrix is a horizontal line, say $y=k$. For a parabola with a horizontal directrix, the axis of symmetry must be a vertical line. Therefore, the equation of the parabola is of the form $f(x) = ax^2 + bx + c$, where $a \neq 0$.

We are given the equation $f^2(0) + f^2(1) + f^2(2) + 45 = 10f(0) + 8f(1) + 4f(2)$. Rearranging the terms, we get: $f^2(0) - 10f(0) + f^2(1) - 8f(1) + f^2(2) - 4f(2) + 45 = 0$ We can complete the square for each quadratic term in $f(0)$, $f(1)$, and $f(2)$: $(f^2(0) - 10f(0) + 25) + (f^2(1) - 8f(1) + 16) + (f^2(2) - 4f(2) + 4) + 45 - 25 - 16 - 4 = 0$ $(f(0) - 5)^2 + (f(1) - 4)^2 + (f(2) - 2)^2 + 45 - 45 = 0$ $(f(0) - 5)^2 + (f(1) - 4)^2 + (f(2) - 2)^2 = 0$

Since the square of a real number is non-negative, the sum of squares is zero if and only if each term is zero. Thus, we have: $f(0) - 5 = 0 \implies f(0) = 5$ $f(1) - 4 = 0 \implies f(1) = 4$ $f(2) - 2 = 0 \implies f(2) = 2$

Now we use the form $f(x) = ax^2 + bx + c$: $f(0) = a(0)^2 + b(0) + c = c = 5$ $f(1) = a(1)^2 + b(1) + c = a + b + c = 4$ $f(2) = a(2)^2 + b(2) + c = 4a + 2b + c = 2$

Substitute $c=5$ into the other two equations: $a + b + 5 = 4 \implies a + b = -1$ (1) $4a + 2b + 5 = 2 \implies 4a + 2b = -3$ (2)

From equation (1), $b = -1 - a$. Substitute this into equation (2): $4a + 2(-1 - a) = -3$ $4a - 2 - 2a = -3$ $2a = -1$ $a = -\frac{1}{2}$

Now find $b$: $b = -1 - a = -1 - (-\frac{1}{2}) = -1 + \frac{1}{2} = -\frac{1}{2}$

So the equation of the parabola is $f(x) = -\frac{1}{2}x^2 - \frac{1}{2}x + 5$.

Now let's evaluate the given options: (A) $y = f(x)$ is symmetric about $x = -\frac{1}{2}$. The axis of symmetry of a parabola $y = ax^2 + bx + c$ is $x = -\frac{b}{2a}$. For $f(x) = -\frac{1}{2}x^2 - \frac{1}{2}x + 5$, $a = -\frac{1}{2}$ and $b = -\frac{1}{2}$. The axis of symmetry is $x = -\frac{-\frac{1}{2}}{2(-\frac{1}{2})} = -\frac{-\frac{1}{2}}{-1} = -\frac{1}{2}$. Thus, the parabola is symmetric about $x = -\frac{1}{2}$. Option (A) is correct.

(B) $f(x) < 0 \forall x \in R$. The parabola opens downwards since $a = -\frac{1}{2} < 0$. The vertex is the maximum point. The x-coordinate of the vertex is $x = -\frac{1}{2}$. The y-coordinate of the vertex is $f(-\frac{1}{2}) = -\frac{1}{2}(-\frac{1}{2})^2 - \frac{1}{2}(-\frac{1}{2}) + 5 = -\frac{1}{2}(\frac{1}{4}) + \frac{1}{4} + 5 = -\frac{1}{8} + \frac{2}{8} + 5 = \frac{1}{8} + 5 = \frac{41}{8}$. The maximum value of $f(x)$ is $\frac{41}{8}$. Since the maximum value is positive, $f(x)$ is not always negative. For example, $f(0) = 5 > 0$. Option (B) is incorrect.

(C) $\ln|f(x)|$ is one-one function. A function is one-one if $f(x_1) = f(x_2)$ implies $x_1 = x_2$. The parabola $f(x) = -\frac{1}{2}x^2 - \frac{1}{2}x + 5$ is symmetric about $x = -\frac{1}{2}$. For any $\delta \neq 0$, $f(-\frac{1}{2} + \delta) = f(-\frac{1}{2} - \delta)$. For instance, $f(0) = 5$ and $f(-1) = -\frac{1}{2}(-1)^2 - \frac{1}{2}(-1) + 5 = -\frac{1}{2} + \frac{1}{2} + 5 = 5$. Since $f(0) = f(-1) = 5$ and $0 \neq -1$, $f(x)$ is not one-one. The function $\ln|u|$ is not one-one on $R \setminus \{0\}$; it is one-one on $(0, \infty)$ and $(-\infty, 0)$. However, the composite function $\ln|f(x)|$ requires $f(x)$ to take values such that $|f(x)|$ is in the domain of $\ln$, i.e., $|f(x)| > 0$ or $f(x) \neq 0$. Since $f(0)=5$ and $f(-1)=5$, $\ln|f(0)| = \ln|5| = \ln 5$ and $\ln|f(-1)| = \ln|5| = \ln 5$. Thus, $\ln|f(0)| = \ln|f(-1)|$ for $0 \neq -1$. Therefore, $\ln|f(x)|$ is not a one-one function. Option (C) is incorrect.

(D) range of $f(x)$ is $(-\infty, \frac{41}{8}]$. As calculated in (B), the parabola opens downwards and has a maximum value at the vertex $(-\frac{1}{2}, \frac{41}{8})$. The range of $f(x)$ is $(-\infty, \text{maximum value}] = (-\infty, \frac{41}{8}]$. Option (D) is correct.

Both options (A) and (D) are correct.