Question
Question: Express $y = \cos^{-1}(2x^{2}-1)$ in terms of $\cos^{-1}x$. ...
Express y=cos−1(2x2−1) in terms of cos−1x.
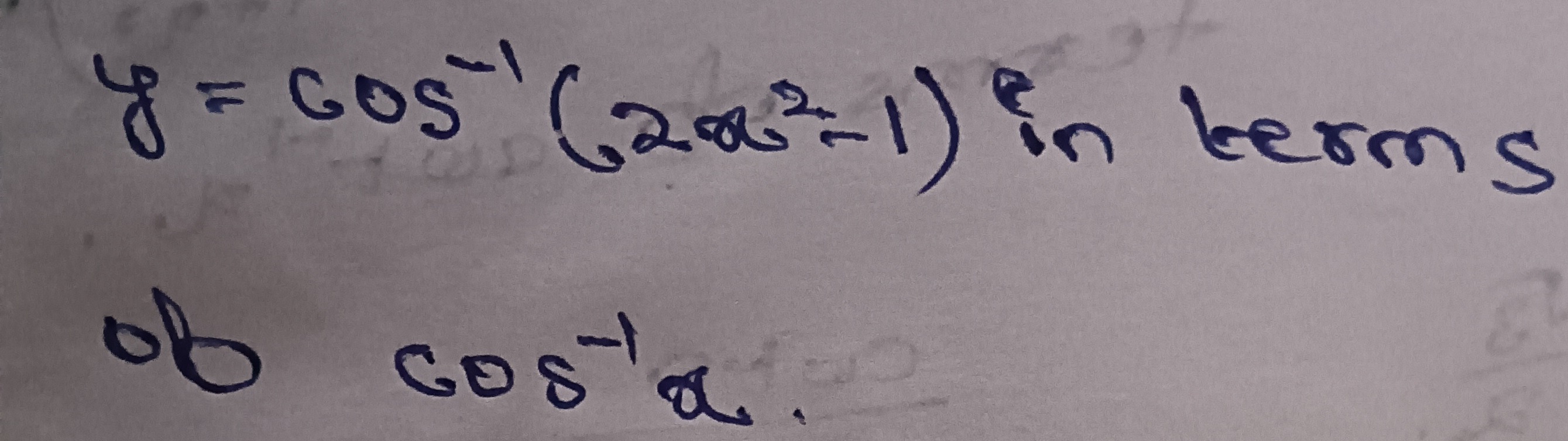
2cos−1x
2π−2cos−1x
2cos−1(∣x∣)
cos−1x
2cos−1(∣x∣)
Solution
Let θ=cos−1x. Then x=cosθ, where 0≤θ≤π. Substituting x=cosθ into the given equation: y=cos−1(2(cosθ)2−1) y=cos−1(2cos2θ−1)
Using the double angle identity cos(2θ)=2cos2θ−1: y=cos−1(cos(2θ))
We know that cos−1(cosz)=z if 0≤z≤π, and cos−1(cosz)=2π−z if π<z≤2π. In our case, z=2θ. Since 0≤θ≤π, the range of 2θ is [0,2π].
Case 1: 0≤2θ≤π. This implies 0≤θ≤2π. Since θ=cos−1x, this means 0≤cos−1x≤2π, which corresponds to 0≤x≤1. In this case, y=2θ=2cos−1x.
Case 2: π<2θ≤2π. This implies 2π<θ≤π. Since θ=cos−1x, this means 2π<cos−1x≤π, which corresponds to −1≤x<0. In this case, y=2π−2θ=2π−2cos−1x.
Combining both cases, we can write the solution piecewise: y={2cos−1x2π−2cos−1xif 0≤x≤1if −1≤x<0
We can express this more compactly using the absolute value function. For x∈[−1,1]: If x≥0, then ∣x∣=x, and 2cos−1(∣x∣)=2cos−1x. If x<0, then ∣x∣=−x, and 2cos−1(∣x∣)=2cos−1(−x). Using the property cos−1(−x)=π−cos−1x, we get 2(π−cos−1x)=2π−2cos−1x.
Thus, the expression y=2cos−1(∣x∣) covers both cases.
