Question

$y = 4^{\log_2 \sin x + 9^{\log_3 \cos x}}$

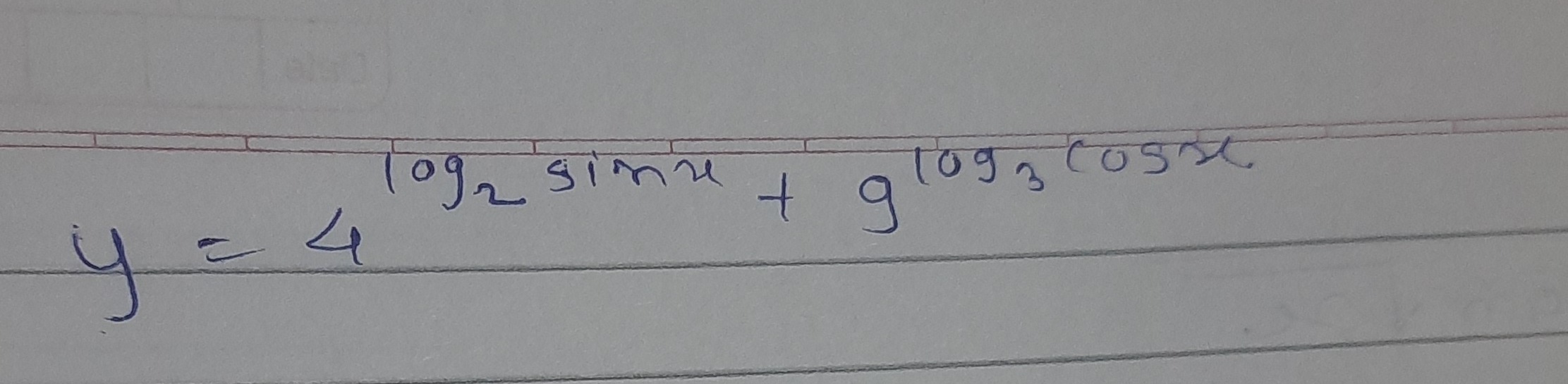
Answer 1

$\frac{dy}{dx} = 2\sin x\cos x\, 4^{\cos^2 x}\left(1 - \ln4\,\sin^2 x\right)$

Answer 2

1. Write $y = 4^{\log_2 \sin x} \cdot 4^{9^{\log_3 \cos x}}$.

2. Simplify:

$$4^{\log_2 \sin x} = \sin^2 x,\quad 9^{\log_3 \cos x} = \cos^2 x,\quad \text{so}\quad 4^{9^{\log_3 \cos x}} = 4^{\cos^2 x}.$$

3. Differentiate $y = \sin^2 x \cdot 4^{\cos^2 x}$ using the product rule and chain rule.

4. Final answer:

$$\frac{dy}{dx} = 2\sin x\cos x\, 4^{\cos^2 x}\left(1 - \ln4\,\sin^2 x\right).$$