Question
Question: Solve the equation: $x^{x+1}=x$...
Solve the equation:
xx+1=x
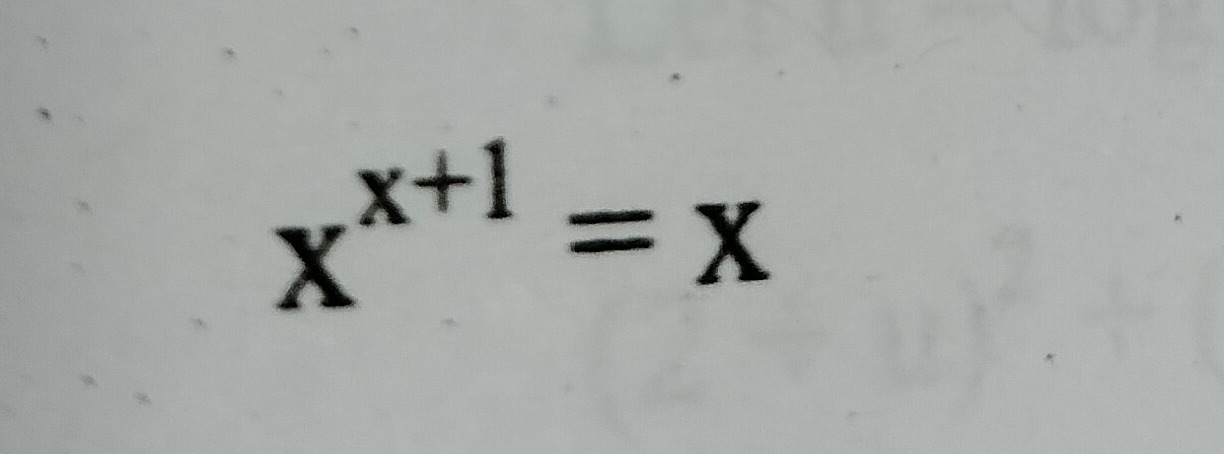
0, 1
Solution
We are asked to solve the equation xx+1=x.
We can rewrite the equation as xx+1−x=0.
Factor out x: x(xx−1)=0.
This gives two possibilities:
- x=0
- xx−1=0, which means xx=1.
Let's check the first possibility, x=0, in the original equation xx+1=x.
Substitute x=0: 00+1=01.
By definition, 01=0.
The right side of the equation is x=0.
So, 01=0, which is 0=0. This is true.
Thus, x=0 is a solution.
Now let's consider the second possibility, xx=1.
We need to find the values of x that satisfy xx=1.
Case 1: The base is 1.
If x=1, then 11=1. This is true.
So x=1 is a solution to xx=1.
Let's check x=1 in the original equation xx+1=x.
Substitute x=1: 11+1=12=1.
The right side is x=1.
So, 12=1, which is 1=1. This is true.
Thus, x=1 is a solution to the original equation.
Case 2: The exponent is 0.
The equation is xx=1. The exponent is x. If x=0, the exponent is 0.
However, if x=0, the base is also 0, leading to 00.
The expression 00 is typically considered indeterminate in calculus, but it is often defined as 1 in combinatorics and other areas.
If we were to define 00=1, then x=0 would be a solution to xx=1.
But we already considered x=0 directly in the original equation and found it is a solution.
The step x(xx−1)=0 assumes xx is defined when x=0.
The equation xx=1 is derived from xx+1=x by dividing by x, which is valid only if x=0.
So, when solving xx=1, we are looking for solutions where x=0.
For x=0, xx=1 means the exponent x must be 0, but this contradicts x=0.
Case 3: The base is -1 and the exponent is an even integer.
Let x=−1. The equation is (−1)−1=1.
(−1)−1=(−1)11=−11=−1.
So, −1=1, which is false.
Thus, x=−1 is not a solution to xx=1.
Let's check x=−1 in the original equation xx+1=x.
Substitute x=−1: (−1)−1+1=(−1)0.
If we define a0=1 for a=0, then (−1)0=1.
The right side is x=−1.
So, 1=−1, which is false.
Thus, x=−1 is not a solution to the original equation.
Let's consider the domain of the expression xx+1.
The expression ab is generally defined as eblna. This requires the base a to be positive, i.e., x>0.
If we restrict x>0, the equation xx+1=x becomes xx+1=x1.
Since the base x is positive and not equal to 1 (if x=1, it is a solution as checked), we can equate the exponents:
x+1=1
x=0.
This contradicts the assumption x>0.
So, under the restriction x>0, the only solution is x=1.
However, the problem does not state any restriction on x. We need to consider other possible values of x for which xx+1 is defined.
The expression xx+1 is defined for:
- x>0 (standard definition e(x+1)lnx)
- x=0 (as 01=0)
- x<0 if x+1 is a rational number p/q where q is odd.
Let's revisit the solutions we found: x=0 and x=1.
For x=0, 00+1=01=0. The right side is 0. 0=0. x=0 is a solution.
For x=1, 11+1=12=1. The right side is 1. 1=1. x=1 is a solution.
Are there any other solutions?
We derived the equation xx=1 by assuming x=0.
Let's consider x<0. Let x=−y where y>0.
The equation xx=1 becomes (−y)−y=1.
(−y)y1=1.
(−y)y=1.
Let y=p/q where p,q are positive integers with gcd(p,q)=1.
(−p/q)p/q=1.
For (−p/q)p/q to be a real number, the denominator q must be odd.
Then (−p/q)p/q=(\rootq\of−p/q)p=(−\rootq\ofp/q)p.
(−\rootq\ofp/q)p=1.
If p is even, p=2k for some integer k≥1 (since y>0, p>0).
(−\rootq\ofp/q)2k=((\rootq\ofp/q)2)k=(\rootq\of(p/q)2)k=1.
Since p/q>0, \rootq\of(p/q)2>0.
So (\rootq\of(p/q)2)k=1 implies \rootq\of(p/q)2=1 (if k≥1).
(p/q)2=1q=1.
p2=q2. Since p,q are positive, p=q.
Since gcd(p,q)=1, this implies p=1 and q=1.
So y=p/q=1/1=1.
This gives x=−y=−1.
We already checked x=−1 in the original equation and found it is not a solution.
If p is odd, p=2k+1 for some integer k≥0.
(−\rootq\ofp/q)2k+1=−(\rootq\ofp/q)2k+1=1.
(\rootq\ofp/q)2k+1=−1.
Since p/q>0, \rootq\ofp/q>0.
A positive number raised to any power is positive.
So (\rootq\ofp/q)2k+1>0.
This means (\rootq\ofp/q)2k+1=−1 has no solution.
So, the equation xx=1 has no solutions for x<0.
The equation xx=1 has only one solution x=1 for x=0.
The solutions to x(xx−1)=0 are x=0 or x=1.
Let's verify if there are any other cases for xx+1=x for x<0.
Let x=−y where y>0.
(−y)−y+1=−y.
(−y)−(y−1)=−y.
(−y)y−11=−y.
1=−y(−y)y−1.
1=−y(−1)y−1yy−1.
1=−(−1)y−1yy.
1=(−1)yyy.
If y is an integer, y=n for n∈{1,2,3,…}.
1=(−1)nnn.
If n is even, n=2k for k≥1. 1=(−1)2k(2k)2k=(2k)2k. Since 2k≥2, (2k)2k≥22=4. No solution.
If n is odd, n=2k+1 for k≥0. 1=(−1)2k+1(2k+1)2k+1=−(2k+1)2k+1. (2k+1)2k+1=−1. Since 2k+1≥1, (2k+1)2k+1≥1. No solution.
If y=p/q with q odd.
1=(−1)p/q(p/q)p/q.
(−1)p/q=(\rootq\of−1)p=(−1)p.
1=(−1)p(p/q)p/q.
If p is even, 1=(p/q)p/q. This implies p/q=1 (as zz=1 for z>0 implies z=1). So y=1, x=−1. We checked x=−1, not a solution.
If p is odd, 1=−(p/q)p/q. (p/q)p/q=−1. No solution as p/q>0.
The only solutions are x=0 and x=1.
