Question

XW $a \cdot b = a \cdot c \neq b=c \implies a(b-c)=0$ $\rightarrow a \cdot b - ac = 0$ do not cancel the terms from both sides (if a is non-zero then can cancel) variable

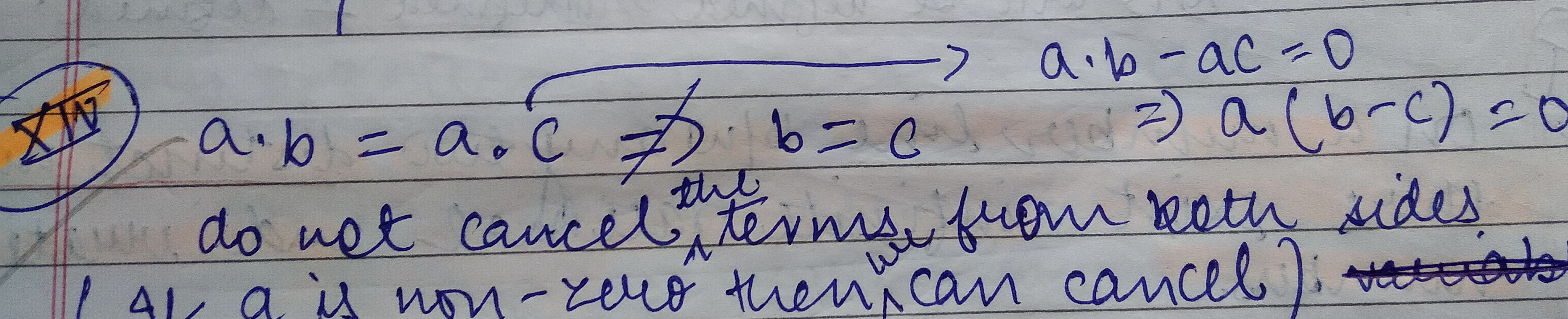
• A. The statement implies that if a non-zero vector 'a' is orthogonal to the difference between vectors 'b' and 'c', then 'b' must be equal to 'c'.
• B. The expression $a \cdot (b-c)=0$ means that vector 'a' is parallel to the vector $(b-c)$.
• C. If $a \cdot b = a \cdot c$, then $b$ must equal $c$, provided $a$ is non-zero.
• D. If $a \cdot b = a \cdot c$, it does not necessarily imply $b=c$ because $a \cdot (b-c)=0$ indicates that $a$ is orthogonal to $(b-c)$.

Answer 1

Answer: (D)

If $a \cdot b = a \cdot c$, it does not necessarily imply $b=c$ because $a \cdot (b-c)=0$ indicates that $a$ is orthogonal to $(b-c)$.

Answer 2

The core of the question lies in understanding the implications of the dot product. The equation $a \cdot b = a \cdot c$ can be rearranged to $a \cdot b - a \cdot c = 0$. Using the distributive property of the dot product, this simplifies to $a \cdot (b - c) = 0$.

This resulting equation, $a \cdot (b - c) = 0$, has a specific geometric interpretation: it means that vector $a$ is orthogonal (perpendicular) to the vector $(b - c)$.

The question highlights that one should not cancel terms directly from both sides if $a$ is non-zero, because this cancellation (which would lead to $b=c$) is only valid if $a$ is non-zero and $b-c$ is also non-zero. The condition $a \cdot (b - c) = 0$ does NOT require $b-c$ to be zero. Instead, it requires $a$ and $(b-c)$ to be perpendicular.

Therefore, it is possible for $a$ to be non-zero and $(b-c)$ to be non-zero, yet their dot product is zero due to their orthogonality. This directly demonstrates that $b$ does not necessarily have to equal $c$ even if $a \cdot b = a \cdot c$.

For instance, consider $\vec{a} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$, $\vec{b} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$, and $\vec{c} = \begin{pmatrix} 2 \\ 5 \end{pmatrix}$. Here, $\vec{b} \neq \vec{c}$. $\vec{a} \cdot \vec{b} = (1)(2) + (0)(3) = 2$. $\vec{a} \cdot \vec{c} = (1)(2) + (0)(5) = 2$. So, $\vec{a} \cdot \vec{b} = \vec{a} \cdot \vec{c}$. Also, $\vec{b} - \vec{c} = \begin{pmatrix} 0 \\ -2 \end{pmatrix}$. $\vec{a} \cdot (\vec{b} - \vec{c}) = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ -2 \end{pmatrix} = (1)(0) + (0)(-2) = 0$. This example shows that $a \cdot b = a \cdot c$ holds true, $b \neq c$ holds true, and $a \cdot (b-c) = 0$ holds true because $a$ is orthogonal to $(b-c)$.