Solveeit Logo
Login

Question

Question: xv) $\frac{1+\cot \theta+\csc \theta}{1-\cot \theta+\csc \theta}=\frac{\csc \theta+\cot \theta-1}{\c...

xv) 1+cot⁡θ+csc⁡θ1−cot⁡θ+csc⁡θ=csc⁡θ+cot⁡θ−1cot⁡θ−csc⁡θ+1\frac{1+\cot \theta+\csc \theta}{1-\cot \theta+\csc \theta}=\frac{\csc \theta+\cot \theta-1}{\cot \theta-\csc \theta+1}

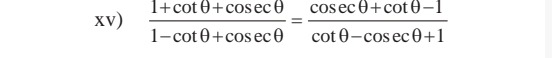
Answer

The given equation is an identity; it holds true for all θ\theta satisfying:

sin⁡θ≠0,sin⁡θ−cos⁡θ+1≠0,sin⁡θ+cos⁡θ−1≠0.\sin\theta\neq 0,\quad \sin\theta-\cos\theta+1\neq 0,\quad \sin\theta+\cos\theta-1\neq 0.
Explanation

Solution

Replace cot⁡θ\cot\theta and csc⁡θ\csc\theta by their expressions in terms of sin⁡θ\sin\theta and cos⁡θ\cos\theta; simplify both sides; the equation reduces to an identity 2sin⁡θcos⁡θ=2sin⁡θcos⁡θ2\sin\theta\cos\theta=2\sin\theta\cos\theta with conditions that the denominators are nonzero.