Question

$x^{\log_a 5} = \frac{1}{2}$

Taking log on both sides to the base 'k'

$\log_a 5 \log_k x = \log_k (\frac{1}{2})$

$\frac{\log_k 5}{\log_k a} \log_k x = \log_k (\frac{1}{2})$

$\frac{\log_k x}{\log_k a} = \frac{\log_k (\frac{1}{2})}{\log_k (5)}$

$\log_a x = \log_5 (\frac{1}{2})$

$\log_a x = \log_5 (2)^{-1}$

$\log_a x = -\log_5 2$

$\log_a x = -\log_5 2$

$x = \frac{a}{2^{-\log_5 a}}$

Is this correct?

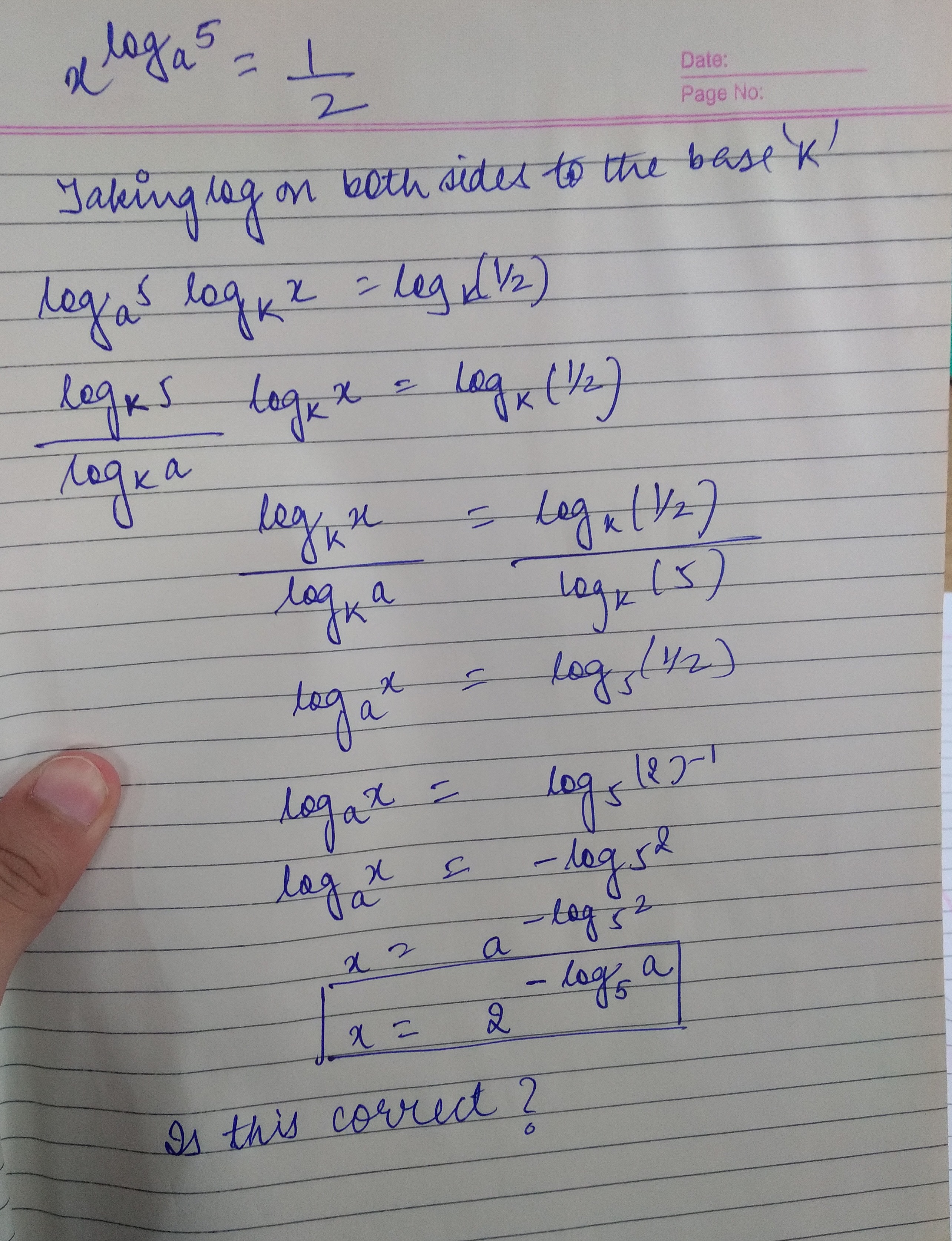
Answer 1

The provided solution is incorrect. The correct solution is $x = a^{-\log_5 2}$ or equivalently $x = 2^{-\log_5 a}$.

Answer 2

The derivation steps are correct up to $\log_a x = -\log_5 2$.

To convert this to exponential form, we use the definition $\log_b y = z \iff y = b^z$. Applying this, we get: $x = a^{-\log_5 2}$

This can be rewritten using logarithm properties: $x = a^{-\log_5 2} = 2^{-\log_5 a}$

The user's final answer $x = \frac{a}{2^{-\log_5 a}}$ simplifies to $x = a \cdot 2^{\log_5 a}$, which is incorrect.