Question

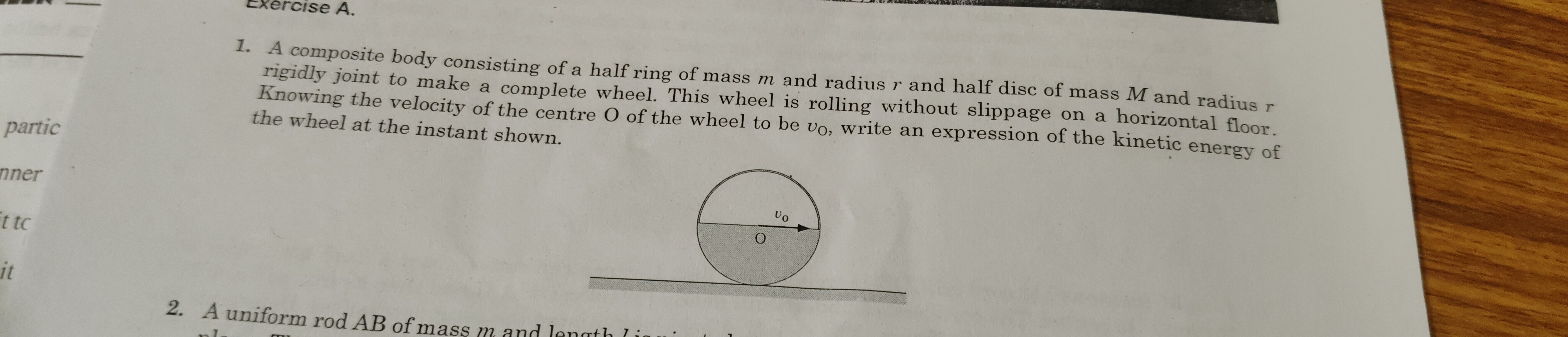
A composite body consisting of a half ring of mass m and radius r and half disc of mass M and radius r rigidly joint to make a complete wheel. This wheel is rolling without slippage on a horizontal floor. Knowing the velocity of the centre O of the wheel to be $v_0$, write an expression of the kinetic energy of the wheel at the instant shown.

Answer 1

$\frac{1}{2} \left(2m + \frac{3M}{2}\right) v_0^2$

Answer 2

The problem asks for the kinetic energy of a composite wheel rolling without slippage. The wheel consists of a half ring of mass m and radius r, and a half disc of mass M and radius r, rigidly joined. The velocity of the center O of the wheel is given as $v_0$.

1. Total Mass of the Wheel: The total mass of the composite wheel is the sum of the masses of the half ring and the half disc: $M_{total} = m + M$

2. Moment of Inertia about the Center O: The moment of inertia of the composite wheel about its geometric center O (perpendicular to the plane of the wheel) is the sum of the moments of inertia of the half ring and the half disc about O.

• Moment of inertia of a half ring of mass m and radius r about its center O is $I_{half\_ring, O} = mr^2$.
• Moment of inertia of a half disc of mass M and radius r about its center O is $I_{half\_disc, O} = \frac{1}{2} Mr^2$.

Therefore, the total moment of inertia about O is: $I_O = mr^2 + \frac{1}{2} Mr^2 = \left(m + \frac{M}{2}\right) r^2$

3. Condition for Rolling Without Slippage: For a wheel rolling without slippage, the linear velocity of its geometric center O ($v_0$) is related to its angular velocity ($\omega$) by the radius r: $v_0 = \omega r \implies \omega = \frac{v_0}{r}$

4. Kinetic Energy of the Rolling Wheel: The total kinetic energy (KE) of a rigid body undergoing combined translational and rotational motion can be expressed as the sum of its translational kinetic energy and rotational kinetic energy about its center of mass. However, if the point O is the geometric center and the velocity of O is given, we can use the formula: $KE = \frac{1}{2} M_{total} v_O^2 + \frac{1}{2} I_O \omega^2$ This formula is valid if O is the center of mass or if O is a fixed point. Even if O is not the center of mass, this form is often used in introductory problems where $v_O$ is given as the "velocity of the center of the wheel" and $I_O$ is the moment of inertia about that geometric center. The additional term $M_{total} \vec{V_O} \cdot (\vec{\omega} \times \vec{r_{CM,O}})$ would be zero if O is the center of mass. However, it is a common simplification in such problems to assume that the given velocity $v_0$ and moment of inertia $I_O$ are sufficient, and the kinetic energy is calculated as the sum of translational KE of the geometric center and rotational KE about the geometric center. This is consistent with the interpretation that $v_0$ is the velocity of the axis of rotation, and $I_O$ is the moment of inertia about that axis.

Substitute the expressions for $M_{total}$, $I_O$, and $\omega$: $KE = \frac{1}{2} (m + M) v_0^2 + \frac{1}{2} \left(m + \frac{M}{2}\right) r^2 \left(\frac{v_0}{r}\right)^2$ $KE = \frac{1}{2} (m + M) v_0^2 + \frac{1}{2} \left(m + \frac{M}{2}\right) r^2 \frac{v_0^2}{r^2}$ $KE = \frac{1}{2} (m + M) v_0^2 + \frac{1}{2} \left(m + \frac{M}{2}\right) v_0^2$

Factor out $\frac{1}{2} v_0^2$: $KE = \frac{1}{2} v_0^2 \left[ (m + M) + \left(m + \frac{M}{2}\right) \right]$ $KE = \frac{1}{2} v_0^2 \left[ m + M + m + \frac{M}{2} \right]$ $KE = \frac{1}{2} v_0^2 \left[ 2m + \frac{3M}{2} \right]$

The expression for the kinetic energy of the wheel is: $KE = \frac{1}{2} \left(2m + \frac{3M}{2}\right) v_0^2$