Question
Question: $|x^2+x+1|+|2x-3|=4x$...
∣x2+x+1∣+∣2x−3∣=4x
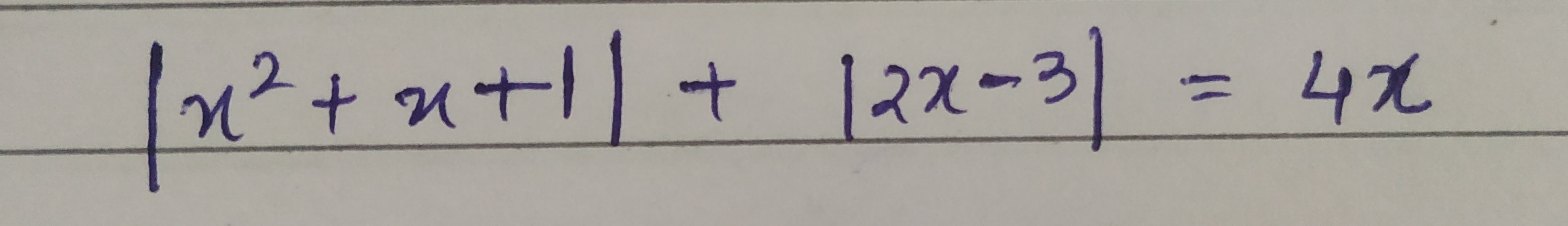
{x=1, 2}
Solution
The given equation is ∣x2+x+1∣+∣2x−3∣=4x.
First, consider the term ∣x2+x+1∣. The quadratic expression x2+x+1 has a discriminant Δ=b2−4ac=12−4(1)(1)=1−4=−3. Since the discriminant is negative and the leading coefficient (1) is positive, the quadratic x2+x+1 is always positive for all real values of x. Therefore, ∣x2+x+1∣=x2+x+1 for all x∈R.
The equation becomes x2+x+1+∣2x−3∣=4x.
The term ∣2x−3∣ depends on the sign of 2x−3. The critical point is when 2x−3=0, which means x=3/2.
Also, note that the left side of the equation is a sum of absolute values, which must be non-negative. Thus, the right side 4x must be non-negative. This implies 4x≥0, so x≥0. Any solution must satisfy this condition.
We consider two cases based on the sign of 2x−3, keeping in mind the condition x≥0. The critical point x=3/2 divides the domain x≥0 into two intervals: [0,3/2) and [3/2,∞).
Case 1: 0≤x<3/2.
In this interval, 2x−3<0, so ∣2x−3∣=−(2x−3)=3−2x.
The equation becomes:
x2+x+1+(3−2x)=4x
x2−x+4=4x
x2−5x+4=0
Factoring the quadratic equation:
(x−1)(x−4)=0
This gives potential solutions x=1 or x=4.
We must check if these potential solutions satisfy the condition for this case, which is 0≤x<3/2.
For x=1: 0≤1<3/2 (True). So x=1 is a valid solution in this case.
For x=4: 0≤4<3/2 (False, since 4<3/2). So x=4 is not a valid solution in this case.
Case 2: x≥3/2.
In this interval, 2x−3≥0, so ∣2x−3∣=2x−3.
The equation becomes:
x2+x+1+(2x−3)=4x
x2+3x−2=4x
x2−x−2=0
Factoring the quadratic equation:
(x−2)(x+1)=0
This gives potential solutions x=2 or x=−1.
We must check if these potential solutions satisfy the condition for this case, which is x≥3/2.
For x=2: 2≥3/2 (True, since 2=4/2). So x=2 is a valid solution in this case.
For x=−1: −1≥3/2 (False). So x=−1 is not a valid solution in this case.
The potential solutions obtained from both cases are x=1 and x=2. Both of these solutions satisfy the overall condition x≥0 (since 1≥0 and 2≥0).
Finally, we verify the solutions by substituting them back into the original equation:
For x=1:
∣12+1+1∣+∣2(1)−3∣=∣3∣+∣−1∣=3+1=4.
4x=4(1)=4.
LHS = RHS, so x=1 is a solution.
For x=2:
∣22+2+1∣+∣2(2)−3∣=∣7∣+∣1∣=7+1=8.
4x=4(2)=8.
LHS = RHS, so x=2 is a solution.
Both x=1 and x=2 are solutions to the given equation.
Explanation of the solution:
- Simplify ∣x2+x+1∣ to x2+x+1 as x2+x+1>0 for all real x.
- Note that 4x≥0, so x≥0.
- Split the problem into cases based on the sign of 2x−3, considering x≥0: Case 1 (0≤x<3/2) and Case 2 (x≥3/2).
- Solve the resulting algebraic equations in each case.
- Check if the solutions obtained in each case satisfy the condition for that case.
- The valid solutions are x=1 (from Case 1) and x=2 (from Case 2).
- Verify these solutions in the original equation. Both x=1 and x=2 satisfy the equation.
