Question

The given equation is $x^2+4y^2+4xy-16y+16=0$.

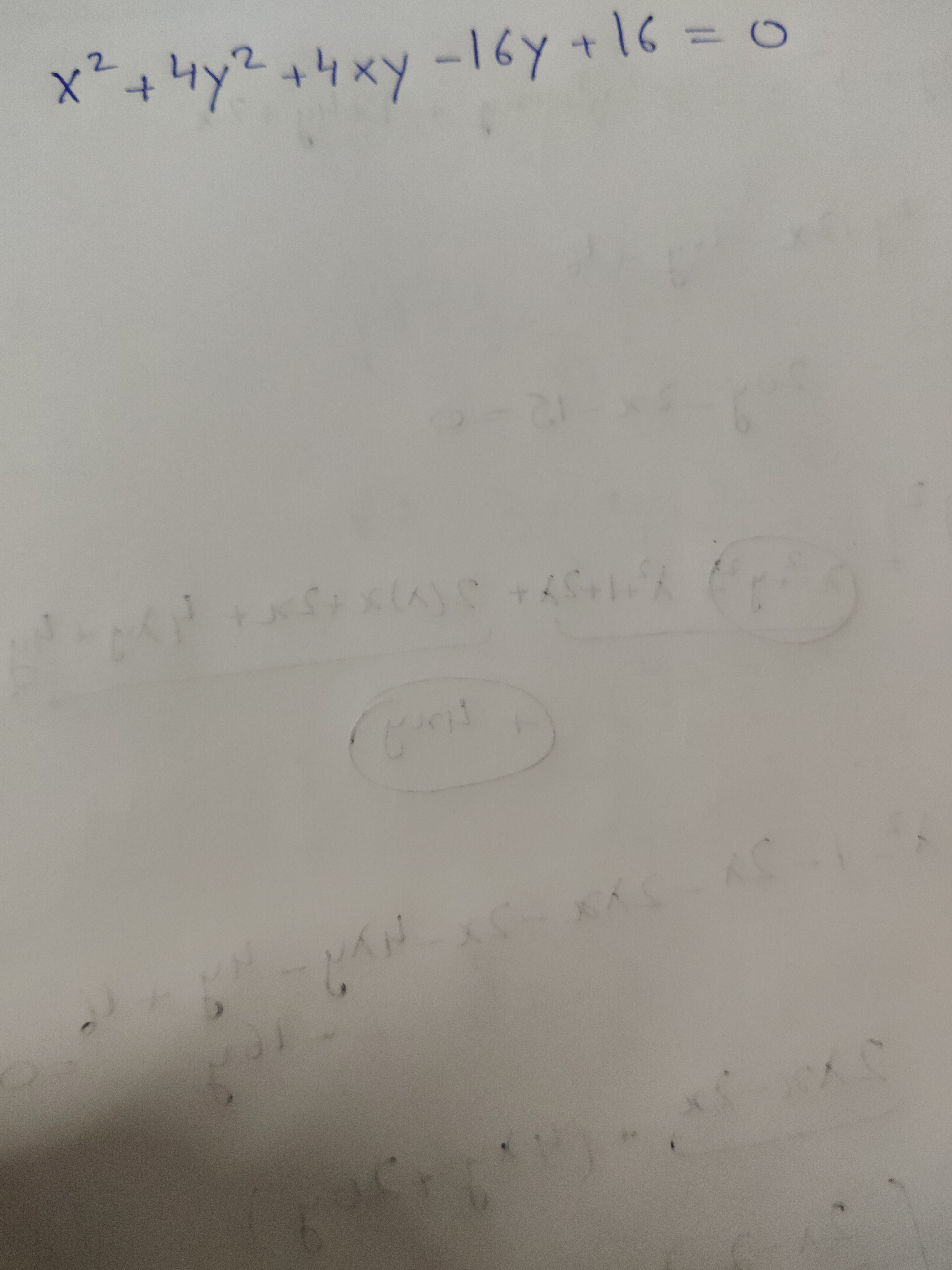
• A. The vertex is at (-2/25, 41/25)
• B. The vertex is at (16/5, 0)
• C. The vertex is at (0, 1)
• D. The vertex is at (-1, 2)

Answer 1

Answer: (A)

The vertex is at (-2/25, 41/25).

Answer 2

The given equation is $x^2+4y^2+4xy-16y+16=0$. This can be rewritten as $(x+2y)^2 - 16y + 16 = 0$. This is the equation of a parabola. The axis of the parabola is parallel to $x+2y=0$. The slope of the axis is $-1/2$. The tangent at the vertex is perpendicular to the axis, so its slope is $2$. Differentiating the equation implicitly with respect to $x$: $2x + 4(y + x\frac{dy}{dx}) + 8y\frac{dy}{dx} - 16\frac{dy}{dx} = 0$ $(4x + 8y - 16)\frac{dy}{dx} = -2x - 4y$ $\frac{dy}{dx} = \frac{-2x - 4y}{4x + 8y - 16} = \frac{-(x+2y)}{2(x+2y-4)}$ Setting $\frac{dy}{dx} = 2$: $\frac{-(x+2y)}{2(x+2y-4)} = 2$ $-(x+2y) = 4(x+2y-4)$ $-(x+2y) = 4(x+2y) - 16$ $16 = 5(x+2y) \implies x+2y = \frac{16}{5}$ This is the equation of the tangent at the vertex. Substitute $x+2y = \frac{16}{5}$ into the simplified equation $(x+2y)^2 - 16y + 16 = 0$: $(\frac{16}{5})^2 - 16y + 16 = 0$ $\frac{256}{25} - 16y + 16 = 0$ $16y = \frac{256}{25} + 16 = \frac{256 + 400}{25} = \frac{656}{25}$ $y = \frac{656}{25 \times 16} = \frac{41}{25}$ Substitute $y$ back into the equation for the tangent line $x+2y = \frac{16}{5}$: $x + 2(\frac{41}{25}) = \frac{16}{5}$ $x + \frac{82}{25} = \frac{80}{25}$ $x = \frac{80}{25} - \frac{82}{25} = -\frac{2}{25}$ The vertex is at $(-\frac{2}{25}, \frac{41}{25})$.