Solveeit Logo
Login

Question

Question: $\newline X^{200} \longrightarrow A^{110} + B^{90}$ If the binding energy per nucleon for X, A and ...

X200⟶A110+B90\newline X^{200} \longrightarrow A^{110} + B^{90}

If the binding energy per nucleon for X, A and B is 7.4 MeV, 8.2 MeV and 8.2 MeV respectively, what is the energy released?

A

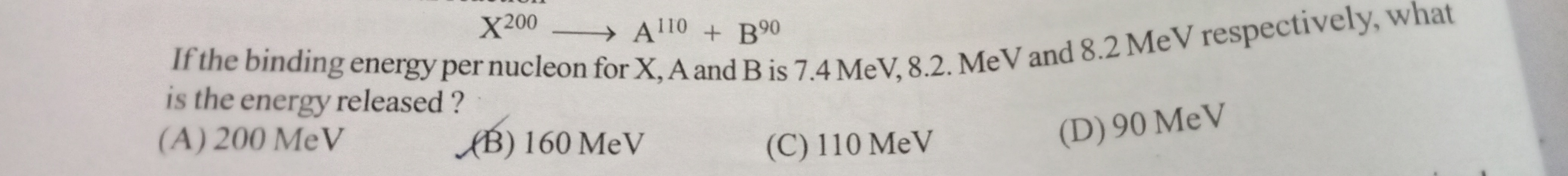
200 MeV

B

160 MeV

C

110 MeV

D

90 MeV

Answer

160 MeV

Explanation

Solution

The energy released in a nuclear reaction is the difference between the total binding energy of the products and the total binding energy of the reactants.

The given nuclear reaction is: X200⟶A110+B90X^{200} \longrightarrow A^{110} + B^{90}

Where:

  • AX=200A_X = 200 (mass number of X)
  • AA=110A_A = 110 (mass number of A)
  • AB=90A_B = 90 (mass number of B)

The binding energy per nucleon values are:

  • BEavg,X=7.4 MeVBE_{avg, X} = 7.4 \text{ MeV}
  • BEavg,A=8.2 MeVBE_{avg, A} = 8.2 \text{ MeV}
  • BEavg,B=8.2 MeVBE_{avg, B} = 8.2 \text{ MeV}

The total binding energy of a nucleus is calculated as: Total Binding Energy = (Binding Energy per nucleon) ×\times (Mass number)

  1. Calculate the total binding energy of the reactant (X): BEX=AX×BEavg,X=200×7.4 MeV=1480 MeVBE_X = A_X \times BE_{avg, X} = 200 \times 7.4 \text{ MeV} = 1480 \text{ MeV}

  2. Calculate the total binding energy of the product (A): BEA=AA×BEavg,A=110×8.2 MeV=902 MeVBE_A = A_A \times BE_{avg, A} = 110 \times 8.2 \text{ MeV} = 902 \text{ MeV}

  3. Calculate the total binding energy of the product (B): BEB=AB×BEavg,B=90×8.2 MeV=738 MeVBE_B = A_B \times BE_{avg, B} = 90 \times 8.2 \text{ MeV} = 738 \text{ MeV}

  4. Calculate the energy released (Q): The energy released in a nuclear reaction is given by: Q=(Total Binding Energy of Products)−(Total Binding Energy of Reactants)Q = (\text{Total Binding Energy of Products}) - (\text{Total Binding Energy of Reactants}) Q=(BEA+BEB)−BEXQ = (BE_A + BE_B) - BE_X Q=(902 MeV+738 MeV)−1480 MeVQ = (902 \text{ MeV} + 738 \text{ MeV}) - 1480 \text{ MeV} Q=1640 MeV−1480 MeVQ = 1640 \text{ MeV} - 1480 \text{ MeV} Q=160 MeVQ = 160 \text{ MeV}

Alternatively, we can express the energy released as: Q=(AA×BEavg,A+AB×BEavg,B)−(AX×BEavg,X)Q = (A_A \times BE_{avg, A} + A_B \times BE_{avg, B}) - (A_X \times BE_{avg, X}) Q=(110×8.2 MeV+90×8.2 MeV)−(200×7.4 MeV)Q = (110 \times 8.2 \text{ MeV} + 90 \times 8.2 \text{ MeV}) - (200 \times 7.4 \text{ MeV}) Since BEavg,A=BEavg,B=8.2 MeVBE_{avg, A} = BE_{avg, B} = 8.2 \text{ MeV}, we can factor it out: Q=(110+90)×8.2 MeV−200×7.4 MeVQ = (110 + 90) \times 8.2 \text{ MeV} - 200 \times 7.4 \text{ MeV} Q=200×8.2 MeV−200×7.4 MeVQ = 200 \times 8.2 \text{ MeV} - 200 \times 7.4 \text{ MeV} Q=200×(8.2−7.4) MeVQ = 200 \times (8.2 - 7.4) \text{ MeV} Q=200×0.8 MeVQ = 200 \times 0.8 \text{ MeV} Q=160 MeVQ = 160 \text{ MeV}

The energy released is 160 MeV.