Question

If $x^2 + y^2 = r^2$, then $\frac{|y_2|}{(1+y_1^2)^{3/2}} =$

Where $y_1 = \frac{dy}{dx}$ and $y_2 = \frac{d^2y}{dx^2}$

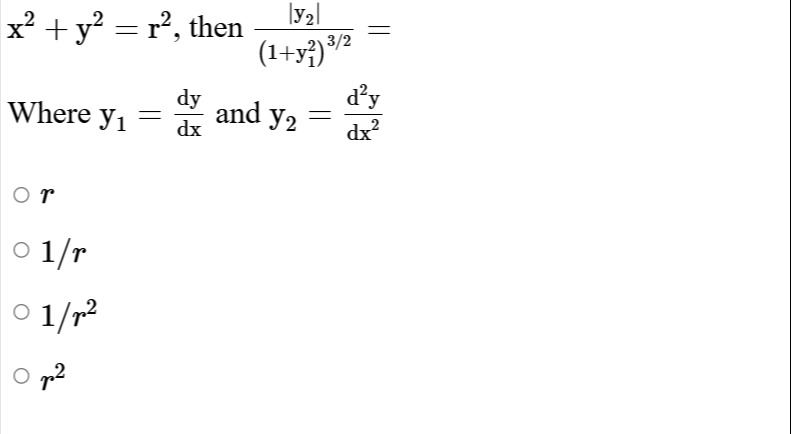
• A. r
• B. 1/r
• C. 1/r^2
• D. r^2

Answer 1

Answer: (B)

1/r

Answer 2

The expression $\frac{|y_2|}{(1+y_1^2)^{3/2}}$ represents the formula for the curvature of a curve. The given equation $x^2+y^2=r^2$ describes a circle of radius $r$. The curvature of a circle is constant and equal to the reciprocal of its radius, which is $1/r$.

To verify this:

1. Differentiate $x^2 + y^2 = r^2$ implicitly with respect to $x$: $2x + 2y y_1 = 0 \implies y_1 = -\frac{x}{y}$.
2. Differentiate $y_1$ with respect to $x$ to find $y_2$: $y_2 = \frac{d}{dx}\left(-\frac{x}{y}\right) = \frac{(-1)(y) - (-x)(y_1)}{y^2} = \frac{-y + x(-\frac{x}{y})}{y^2} = \frac{-y^2 - x^2}{y^3} = -\frac{x^2+y^2}{y^3}$. Since $x^2+y^2=r^2$, we get $y_2 = -\frac{r^2}{y^3}$.
3. Calculate $1+y_1^2$: $1+y_1^2 = 1 + \left(-\frac{x}{y}\right)^2 = 1 + \frac{x^2}{y^2} = \frac{y^2+x^2}{y^2} = \frac{r^2}{y^2}$.
4. Calculate $(1+y_1^2)^{3/2}$: $(1+y_1^2)^{3/2} = \left(\frac{r^2}{y^2}\right)^{3/2} = \left(\left(\frac{r}{y}\right)^2\right)^{3/2} = \left|\frac{r}{y}\right|^3 = \frac{r^3}{|y|^3}$ (since $r>0$).
5. Calculate $|y_2|$: $|y_2| = \left|-\frac{r^2}{y^3}\right| = \frac{r^2}{|y|^3}$.
6. Substitute into the curvature formula: $\frac{|y_2|}{(1+y_1^2)^{3/2}} = \frac{\frac{r^2}{|y|^3}}{\frac{r^3}{|y|^3}} = \frac{r^2}{r^3} = \frac{1}{r}$.