Question

$|x^2-x-6|=x+2$

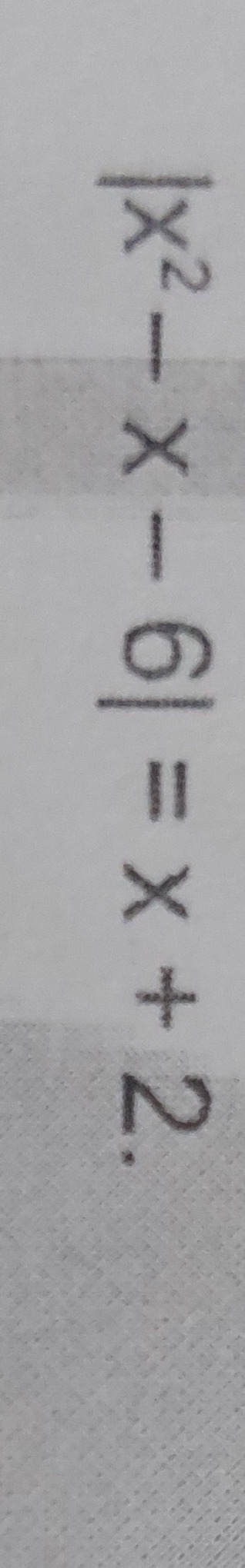
Answer 1

The solutions are $x = -2, 2, 4$.

Answer 2

The equation $|x^2-x-6|=x+2$ requires $x+2 \ge 0$, so $x \ge -2$.

Split the equation into two cases based on the definition of absolute value: $x^2-x-6 = x+2$ or $x^2-x-6 = -(x+2)$.

Solve the first case $x^2-x-6 = x+2 \implies x^2-2x-8=0 \implies (x-4)(x+2)=0$, yielding $x=4, x=-2$. Both satisfy $x \ge -2$.

Solve the second case $x^2-x-6 = -(x+2) \implies x^2-x-6 = -x-2 \implies x^2-4=0 \implies x=\pm 2$. Both satisfy $x \ge -2$.

The set of solutions is the union of solutions from both cases that satisfy the initial condition: $\{-2, 2, 4\}$.