Question
Question: $(x^2-x-1)(x^2-x-7)<-5$...
(x2−x−1)(x2−x−7)<−5
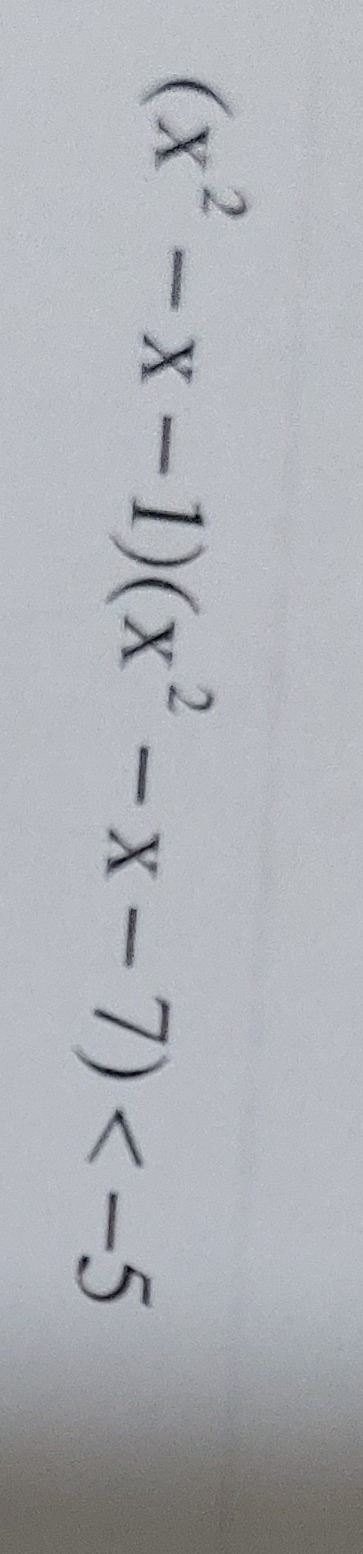
(−2,−1)∪(2,3)
Solution
Let y=x2−x. Substituting this into the inequality, we get: (y−1)(y−7)<−5
Expand the left side: y2−7y−y+7<−5 y2−8y+7<−5
Add 5 to both sides: y2−8y+7+5<0 y2−8y+12<0
To solve this quadratic inequality, we find the roots of the corresponding quadratic equation y2−8y+12=0. Factoring the quadratic: (y−2)(y−6)=0 The roots are y=2 and y=6.
Since the coefficient of y2 is positive (1 > 0), the parabola opens upwards. The inequality y2−8y+12<0 holds for the values of y between the roots. So, the solution for y is 2<y<6.
Now, substitute back y=x2−x: 2<x2−x<6
This is a compound inequality, which can be split into two separate inequalities:
- x2−x>2
- x2−x<6
Let's solve the first inequality: x2−x>2 x2−x−2>0 Find the roots of x2−x−2=0: (x−2)(x+1)=0 The roots are x=2 and x=−1. Since the inequality is x2−x−2>0 and the parabola x2−x−2 opens upwards, the solution is outside the roots: x<−1 or x>2. In interval notation: (−∞,−1)∪(2,∞).
Now, let's solve the second inequality: x2−x<6 x2−x−6<0 Find the roots of x2−x−6=0: (x−3)(x+2)=0 The roots are x=3 and x=−2. Since the inequality is x2−x−6<0 and the parabola x2−x−6 opens upwards, the solution is between the roots: −2<x<3. In interval notation: (−2,3).
The solution to the original inequality is the intersection of the solutions to the two inequalities: ((−∞,−1)∪(2,∞))∩(−2,3)
We find the intersection by considering the intervals on a number line. The interval (−2,3) is the region between -2 and 3. The set (−∞,−1)∪(2,∞) is the region to the left of -1 or to the right of 2.
The intersection of (−2,3) and (−∞,−1) is (−2,−1). The intersection of (−2,3) and (2,∞) is (2,3).
The union of these intersections is the final solution: (−2,−1)∪(2,3).
