Question
Question: \(x\) and \(y\) displacements of a particle are given as \(x\left( t \right) = a\sin \omega t\) \(y\...
x and y displacements of a particle are given as x(t)=asinωt y(t)=asin2ωt. Its trajectory will look like.
(A)
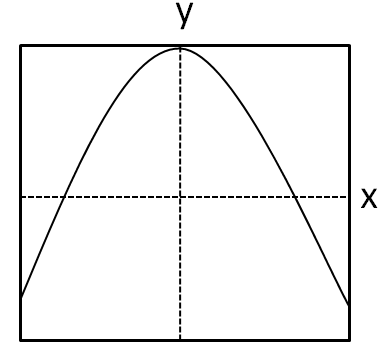
(B)
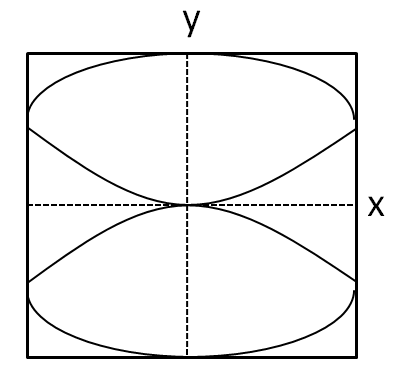
(C)
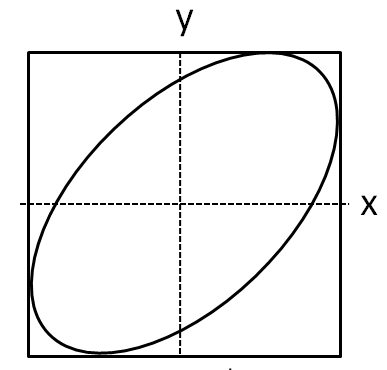
(D)
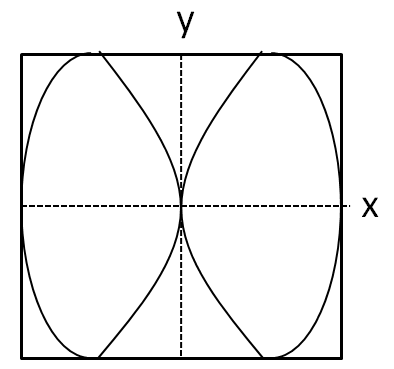
Solution
We have been given an implicit relation between the two displacements. To solve this question, we need to obtain the explicit relation between them. Then we can check for the symmetries about the axes, and the point of intersection with the axes to get the correct answer.
Complete step-by-step solution:
The equation of the displacement of the particle along the x direction is given as
x(t)=asinωt
⇒sinωt=ax....................(1)
Also, the equation of the displacement of the particle along the y direction is given as
y(t)=asin2ωt
Now, we know that sin2θ=2sinθcosθ. Therefore we can write the above equations
y=2asinωtcosωt............……..(2)
We know that
cos2ωt+sin2ωt=1
⇒cos2ωt=1−sin2ωt
Taking square root both the sides, we get
cosωt=1−sin2ωt ………... (3)
Substituting (3) in (2) we get
y=2asinωt1−sin2ωt.................(4)
Substituting (1) in (4) we get
y=2a(ax)(1−(ax)2)
⇒y=2(ax)(a2−x2)
On squaring both the sides, we have
y2=2(ax)2(a2−x2)
⇒y2=2(a2a2x2−x4)
Multiplying both sides by a2, we have
a2y2=2(a2x2−x4)
⇒2x4−2a2x2+a2y2=0.....................(5)
This is the required relation between x and y.
Now, we replace x with −x in (5) to get
2(−x)4−2a2(−x)2+a2y2=0
⇒2x4−2a2x2+a2y2=0
So this equation is similar to the equation (5) even after replacing x with −x. So the graph between x and y must be symmetric about the y axis.
Now, we replace y with −y in (5) to get
2x4−2a2x2+a2(−y)2=0
⇒2x4−2a2x2+a2y2=0
This equation is also similar to the equation (5) and therefore the graph between x and y must be symmetric about the x axis.
So the graph is symmetric about both the axes.
The graph given in the option A is symmetric about y axis, but is not symmetric about the x axis.
Hence, the option A is incorrect.
The graph given in the option C is not symmetric about any of the axes.
Hence, the option C is also not correct.
Substituting y=0 in (5) we get
2x4−2a2x2=0
⇒2x2(x2−a2)=0
On solving we get
x=0 and x=±a
So the graph cuts the x axis at three values of the abscissa 0,a,−a.
We can see that the graph given in the option B cuts the x axis at only the origin. So option B is incorrect.
But we see that the graph given in the option D cuts the x axis at three points.
Hence, the correct answer is option C.
Note: The graph of the curve, whose equation is obtained above, is not easy to be sketched. This is evident from its equation. The graph is sketched using the special technique of curve sketching. But we do not need to follow that technique. We just need to check for the points at the axes, and the symmetry for getting the correct answer.
