Question

'X' and 'Y' are two elements which form $X_2Y_3$ and $XY_2$ molecules. If 0.15 mole of $X_2Y_3$ and $XY_2$ weighs 15.9 gm & 9.3 gm respectively. If oxidation state of 'y' in both compounds is +2 than correct options are:

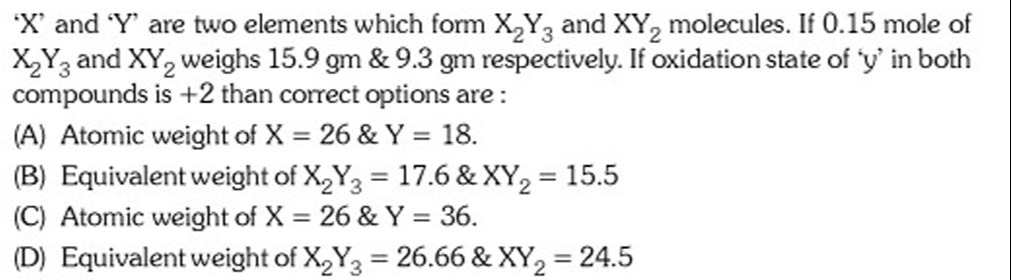
• A. Atomic weight of X = 26 & Y = 18.
• B. Equivalent weight of $X_2Y_3$ = 17.6 & $XY_2$ = 15.5
• C. Atomic weight of X = 26 & Y = 36.
• D. Equivalent weight of $X_2Y_3$ = 26.66 & $XY_2$ = 24.5

Answer 1

Answer: (A), (B)

Options (A) and (B) are correct.

Answer 2

Let the atomic weights of X and Y be A and B respectively.

1. From the compound $X_2Y_3$:

   • Molecular weight = 2A + 3B
   • Given 0.15 mole weighs 15.9 g so: $2A + 3B = \frac{15.9}{0.15} = 106$

2. From the compound $XY_2$:

   • Molecular weight = A + 2B
   • Given 0.15 mole weighs 9.3 g so: $A + 2B = \frac{9.3}{0.15} = 62$

Solving the equations:

Subtracting 2 times the second equation from the first equation: $(2A + 3B) - 2(A + 2B) = 106 - 2(62)$ $2A + 3B - 2A - 4B = 106 - 124$ $-B = -18$ $B = 18$

Plugging B = 18 into the second equation: $A + 2(18) = 62$ $A + 36 = 62$ $A = 26$

Therefore, the atomic weight of X is 26 and the atomic weight of Y is 18.

Equivalent Weight Calculation:

Given that the oxidation state of Y is +2:

• For $X_2Y_3$:

  • Total oxidation by Y = 3 * (+2) = +6
  • So X must be -3 each (since 2*(-3) + 6 = 0)
  • Total electrons involved per molecule = 2 * 3 = 6
  • Equivalent weight = $\frac{Molecular\ weight}{6} = \frac{106}{6} \approx 17.67 \approx 17.6$ g/equivalent

• For $XY_2$:

  • Oxidation: Let X be x; then x + 2*(+2) = 0 gives x = -4
  • Total electrons involved per molecule = 4
  • Equivalent weight = $\frac{Molecular\ weight}{4} = \frac{62}{4} = 15.5$ g/equivalent

Thus, the atomic weights are X = 26 and Y = 18, and the equivalent weights are as calculated.