Question

$(x + 2)(x + 4)(x + 6)(x + 12) + 4x^2 = 0$

Answer 1

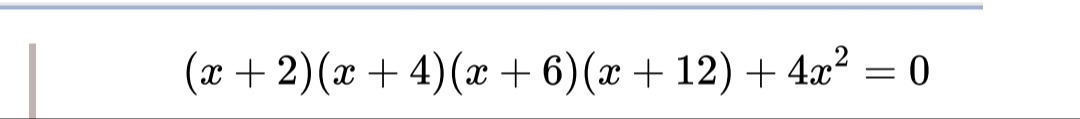
x = -6 \pm 2\sqrt{3}

Answer 2

To solve the equation $(x + 2)(x + 4)(x + 6)(x + 12) + 4x^2 = 0$, we strategically group the terms.

Notice that the product of the constants in one pair, $2 \times 12 = 24$, is equal to the product of the constants in another pair, $4 \times 6 = 24$.

Rearrange the terms: $[(x + 2)(x + 12)][(x + 4)(x + 6)] + 4x^2 = 0$

Expand each pair: $(x + 2)(x + 12) = x^2 + 12x + 2x + 24 = x^2 + 14x + 24$ $(x + 4)(x + 6) = x^2 + 6x + 4x + 24 = x^2 + 10x + 24$

Substitute these back into the equation: $(x^2 + 14x + 24)(x^2 + 10x + 24) + 4x^2 = 0$

Let $y = x^2 + 24$. The equation becomes: $(y + 14x)(y + 10x) + 4x^2 = 0$

Expand the product: $y^2 + 10xy + 14xy + 140x^2 + 4x^2 = 0$ $y^2 + 24xy + 144x^2 = 0$

This expression is a perfect square trinomial: $y^2 + 2(y)(12x) + (12x)^2 = 0$ $(y + 12x)^2 = 0$

Substitute back $y = x^2 + 24$: $(x^2 + 24 + 12x)^2 = 0$ $(x^2 + 12x + 24)^2 = 0$

For this equation to hold, the term inside the parenthesis must be zero: $x^2 + 12x + 24 = 0$

Now, solve this quadratic equation using the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$. Here, $a=1$, $b=12$, $c=24$.

$x = \frac{-12 \pm \sqrt{12^2 - 4 \cdot 1 \cdot 24}}{2 \cdot 1}$ $x = \frac{-12 \pm \sqrt{144 - 96}}{2}$ $x = \frac{-12 \pm \sqrt{48}}{2}$

Simplify $\sqrt{48}$: $\sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}$

Substitute this value back: $x = \frac{-12 \pm 4\sqrt{3}}{2}$ $x = \frac{2(-6 \pm 2\sqrt{3})}{2}$ $x = -6 \pm 2\sqrt{3}$

The solutions are $x = -6 + 2\sqrt{3}$ and $x = -6 - 2\sqrt{3}$.