Question

$x = 1$is the radical axis of two circles which cut each other orthogonally. If ${x^2} + {y^2} = 9$ is the equation of one circle, then the equation of the other circle is
A.${x^2} + {y^2} - 9x + 9 = 0$
B.${x^2} + {y^2} + 18x - 9 = 0$
C.${x^2} + {y^2} - 18x + 9 = 0$
D.${x^2} + {y^2} + 9x + 9 = 0$

Answer 1

Hint : Orthogonal circles cut one another at right angles. Using Pythagoras theorem, two circle of radii r1, r2 whose center are at distance d apart are orthogonal if $r_1^2 + r_2^2 = {d^2}$ and given by the equation $2gg' + 2ff' = c + c'$.
The angle of intersection of two overlapping circles is defined as the angle between their tangents at their intersection points. Where if the angle is ${180^ \circ }$ it is known as tangent and the angle is ${90^ \circ }$then it is orthogonal.

Complete step-by-step answer :
Given the equation of one circle is ${x^2} + {y^2} = 9$ whose center is (0, 0)

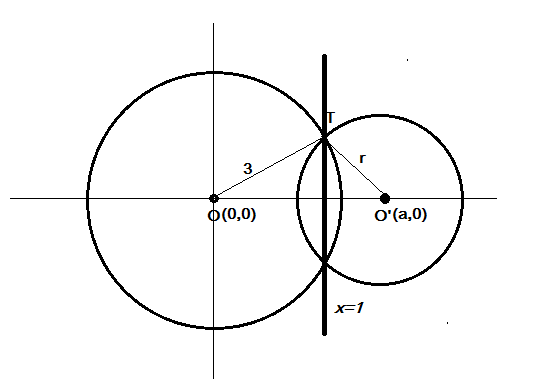
Given the radical axis of two circles$x = 1$, therefore the line joining centers should be perpendicular to$x = 1$
The center of another circle should lie on$y = 0$,
Let the center of another circle be $\left( {a,0} \right)$and the radius $r$,
So the equation of other circle is ${\left( {x - a} \right)^2} + {y^2} = {r^2} - - - - (i)$
Since the given two circles are orthogonal we can write ${a^2} = {r^2} + 9$
We know the center of the two circle are at $\left( {0,0} \right)$ and also their radius being 3 and r respectively
Since the lengths of the tangents from radial axis are equal, hence we get
$\Rightarrow {\left( {1 - a} \right)^2} + 0 - {r^2} = 1 - 9$
This can be written as:

$$\Rightarrow {\left( {1 - a} \right)^2} + 0 - {r^2} = 1 - 9 \\\ \Rightarrow 1 - 2a + {a^2} - {r^2} = - 8 \\\ \Rightarrow {a^2} - {r^2} = 2a - 9 - - (i) \\\$$

We know ${a^2} = {r^2} + 9$ since the circles are orthogonal
$\Rightarrow {a^2} - {r^2} = 9 - - (ii)$
Hence by solving equation (i) and (ii) we can write

$$\Rightarrow 2a - 9 = 9 \\\ \Rightarrow 2a = 18 \\\ \Rightarrow a = 9 \\\$$

Also

$${a^2} - {r^2} = 9 \\\ \Rightarrow {\left( 9 \right)^2} - {r^2} = 9 \\\ \Rightarrow {r^2} = 81 - 9 \\\ \Rightarrow {r^2} = 72 \\\$$

Substituting the values of $a = 9$ and ${r^2} = 72$ in equation (i) as:

$$\Rightarrow {\left( {x - a} \right)^2} + {y^2} = {r^2} \\\ \Rightarrow {\left( {x - 9} \right)^2} + {y^2} = 72 \\\ \Rightarrow {x^2} + 81 - 18x + {y^2} - 72 = 0 \\\ \Rightarrow {x^2} + {y^2} - 18x + 9 = 0 \\\$$

Hence, the equation of the required circle is given as ${x^2} + {y^2} - 18x + 9 = 0$.

So, the correct answer is “Option C”.

Note : Students must not get confused with the two equations of the circle as the coordinates of the center of both the circles are different. Moreover, the radius is varying by a considerable amount. Always try to stick to the fundamental standard equation of the circle i.e., ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$ .