Solveeit Logo
Login

Question

Question: Write the vector representation of the vectors \( A \) and \( B \) with respect to the frame of refe...

Write the vector representation of the vectors AA and BB with respect to the frame of reference shown in the figure.

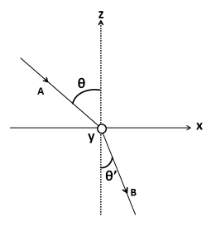
(A) A⃗=Asin⁡θi^−Acos⁡θk^\vec A = A\sin \theta \hat i - A\cos \theta \hat k , B⃗=Bsin⁡θ′j^−Bcos⁡θ′k^\vec B = B\sin \theta '\hat j - B\cos \theta '\hat k
(B) A⃗=Asin⁡θi^−Bcos⁡θk^\vec A = A\sin \theta \hat i - B\cos \theta \hat k , B⃗=Asin⁡θ′j^−Bcos⁡θ′k^\vec B = A\sin \theta '\hat j - B\cos \theta '\hat k
(C) A⃗=Bsin⁡θi^−Acos⁡θk^\vec A = B\sin \theta \hat i - A\cos \theta \hat k , B⃗=Bsin⁡θ′j^−Acos⁡θ′k^\vec B = B\sin \theta '\hat j - A\cos \theta '\hat k
(D) A⃗=Bsin⁡θi^−Bcos⁡θk^\vec A = B\sin \theta \hat i - B\cos \theta \hat k , B⃗=Asin⁡θ′j^−Acos⁡θ′k^\vec B = A\sin \theta '\hat j - A\cos \theta '\hat k

Explanation

Solution

Hint : To solve this question, we need to consider the angles of inclination of the vectors with one axis. Then, multiplying the magnitudes with the cosine and the sine of the angle will respectively give the components along that axis and perpendicular to that axis.

Complete step by step answer
The vector AA is lying in the x-z plane. Therefore, it will have two perpendicular components; one along the direction of the x axis, and the other along the direction of z axis.
Separating the vector AA out of the figure given in the question, we have

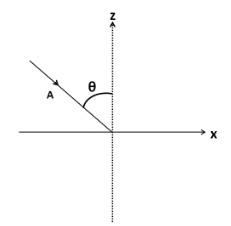
For taking the components, we have to do this vector AA co-initial with the unit vectors, i^\hat i and k^\hat k . Redrawing the above figure, we get

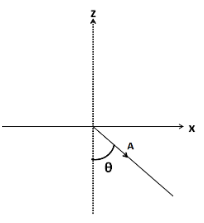
As we can observe, the angle made by vector AA with the x axis is
φ=(π2−θ)\varphi = \left( {\dfrac{\pi }{2} - \theta } \right)
As this angle is in clockwise direction, so we take it to be negative. Therefore
φ=−(π2−θ)\varphi = - \left( {\dfrac{\pi }{2} - \theta } \right) ………………….(1)
Now, the component of AA along the x axis is
Ax=Acos⁡φ{A_x} = A\cos \varphi
From (1)
Ax=Acos⁡[−(π2−θ)]{{\rm A}_x} = A\cos \left[ { - \left( {\dfrac{\pi }{2} - \theta } \right)} \right]
We know that cos⁡(−x)=cos⁡x\cos \left( { - x} \right) = \cos x . Therefore, we get
Ax=Acos⁡(π2−θ){{\rm A}_x} = A\cos \left( {\dfrac{\pi }{2} - \theta } \right)
⇒Ax=Asin⁡θ\Rightarrow {{\rm A}_x} = A\sin \theta ………………….(2)
Now, the component along the z axis is
Az=Asin⁡φ{{\rm A}_z} = A\sin \varphi
From (1)
Az=Asin⁡[−(π2−θ)]{{\rm A}_z} = A\sin \left[ { - \left( {\dfrac{\pi }{2} - \theta } \right)} \right]
We know that sin⁡(−x)=−sin⁡x\sin \left( { - x} \right) = - \sin x . So we get
Az=−Asin⁡(π2−θ){{\rm A}_z} = - A\sin \left( {\dfrac{\pi }{2} - \theta } \right)
⇒Az=−Acos⁡θ\Rightarrow {{\rm A}_z} = - A\cos \theta ………………….(3)
Now, the vector AA can be represented as
A⃗=Axi^+Azk^\vec A = {A_x}\hat i + {A_z}\hat k
From (2) and (3)
A⃗=Asin⁡θi^−Acos⁡θk^\vec A = A\sin \theta \hat i - A\cos \theta \hat k
Now, we separate the vector BB out of the given figure

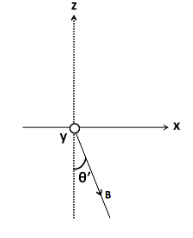
The vector BB is lying in the y-z plane. So it will have two perpendicular components; one along the unit vector j^\hat j , and the other along the unit vector k^\hat k .
Redrawing the above figure in the y-z plane, we have

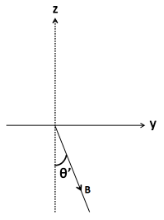
As we can observe, the angle made by vector BB with the y axis is
φ′=(π2−θ′)\varphi ' = \left( {\dfrac{\pi }{2} - \theta '} \right)
As this angle is in clockwise direction, so we take it to be negative. Therefore
φ′=−(π2−θ′)\varphi ' = - \left( {\dfrac{\pi }{2} - \theta '} \right) ………………….(4)
Now, the component of BB along the y axis is
By=Bcos⁡φ′{B_y} = B\cos \varphi '
From (4)
By=Bcos⁡[−(π2−θ′)]{B_y} = B\cos \left[ { - \left( {\dfrac{\pi }{2} - \theta '} \right)} \right]
We know that cos⁡(−x)=cos⁡x\cos \left( { - x} \right) = \cos x . Therefore, we get
By=Bcos⁡(π2−θ′){B_y} = B\cos \left( {\dfrac{\pi }{2} - \theta '} \right)
⇒By=Bsin⁡θ′\Rightarrow {B_y} = B\sin \theta ' ………………….(5)
Now, the component along the z axis is
Bz=Bsin⁡φ′{B_z} = B\sin \varphi '
From (4)
Bz=Bsin⁡[−(π2−θ′)]{B_z} = B\sin \left[ { - \left( {\dfrac{\pi }{2} - \theta '} \right)} \right]
We know that sin⁡(−x)=−sin⁡x\sin \left( { - x} \right) = - \sin x . So we get
Bz=−Bsin⁡(π2−θ′){B_z} = - B\sin \left( {\dfrac{\pi }{2} - \theta '} \right)
⇒Bz=−Bcos⁡θ′\Rightarrow {B_z} = - B\cos \theta ' ………………….(6)
Now, the vector AA can be represented as
B⃗=Byj^+Bzk^\vec B = {B_y}\hat j + {B_z}\hat k
From (5) and (6)
B⃗=Bsin⁡θ′j^−Bcos⁡θ′k^\vec B = B\sin \theta '\hat j - B\cos \theta '\hat k -
Thus, the vector representation of the vectors AA and BB are A⃗=Asin⁡θi^−Acos⁡θk^\vec A = A\sin \theta \hat i - A\cos \theta \hat k and B⃗=Bsin⁡θ′j^−Bcos⁡θ′k^\vec B = B\sin \theta '\hat j - B\cos \theta '\hat k .
Hence, the correct answer is option A.

Note
The vector BB appears to be lying in the x-z plane. But the options show that it has one component along the unit vector j^\hat j . So from there we got to know that the vector BB is in the y-z plane.