Question

Write the vector equation of the plane passing through the point (a, b, c) and parallel to the plane $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$

Answer 1

To solve this question, we will use general equation of a plane where normal vector is $\vec{n}$ and distance $\vec{d}$ the general equation of a plane with normal vector $\vec{n}$ and distance $\vec{d}$ from point of a position vector $\vec{r}$ is given by: $\vec{r}\cdot \vec{n}=\vec{d}$
We will compare this to $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$ and try to get the value of 2 in term of a, b and c. In between while calculation, we will use dot product of two vector.

Complete step-by-step solution:
Dot product of two vector $\vec{p}\text{ and }\vec{q}$ where $p=x\hat{i}+y\hat{j}+z\hat{k}\text{ and q=}x'\hat{i}+y'\hat{j}+z'\hat{k}$ given by
$\vec{p}\cdot \vec{q}=xx'+yy'+zz\text{ }\\!\\!'\\!\\!\text{ }$
The general equation of a plane with normal vector $\vec{n}$ and distance $\vec{d}$ from point of a position vector $\vec{r}$ is given by:
$\vec{r}\cdot \vec{n}=\vec{d}$

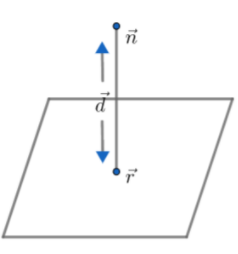
Comparison our given equation from given equation $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$ we get that the normal vector $\vec{n}=\hat{i}+\hat{j}+\hat{k}$ and distance d.
So, we have $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=d\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)}$
Where $\hat{i}+\hat{j}+\hat{k}$ is the normal vector.
We are given that, the point is (a, b, c) then, writing this $\left( a,b,c \right)=a\hat{i}+b\hat{j}+c\hat{k}$ is the position vector of the point (a, b, c).
Position vector of a point (p, q, r) is given as $p\hat{i}+q\hat{j}+r\hat{k}$ because $\vec{r}=a\hat{i}+b\hat{j}+c\hat{k}$ is the position vector of point (a, b, c).
Substituting this $\vec{r}=a\hat{i}+b\hat{j}+c\hat{k}$ in equation (i) we get
$\Rightarrow \left( a\hat{i}+b\hat{j}+c\hat{k} \right)\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=d$
Dot product of two vector $\vec{p}\text{ and }\vec{q}$ where $p=x\hat{i}+y\hat{j}+z\hat{k}\text{ and q=}x'\hat{i}+y'\hat{j}+z'\hat{k}$ given by
$\vec{p}\cdot \vec{q}=xx'+yy'+zz\text{ }\\!\\!'\\!\\!\text{ }$
Using this above to get dot product of above vector, we get:
$\Rightarrow a+b+c=d$
So, we have value of $d=a+b+c$
Substituting value of $d=a+b+c$ in equation (i) we get
$\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=a+b+c\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)}$
This is the vector equation of required plane.
Substituting $\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\text{ }$ in equation (ii) we get:
$\left( x\hat{i}+y\hat{j}+z\hat{k}\text{ } \right)\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=a+b+c\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iii)}$
Both equation (ii) and equation (iii) are our required vector equation of a plane passing through the point (a, b, c) and parallel to the plane $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$

Note: We can also use $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$ as given in the question and substitute d = 2 then, the value of $a+b+c=2$ then, we can directly substitute $a+b+c=2$ in equation (ii) that is $\vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=a+b+c=2\Rightarrow \vec{r}\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$ then, the final answer would be $\left( x\hat{i}+y\hat{j}+z\hat{k}\text{ } \right)\cdot \left( \hat{i}+\hat{j}+\hat{k} \right)=2$ which is required result.