Solveeit Logo
Login

Question

Question: Write the value of \[{{\tan }^{-1}}\dfrac{a}{b}-{{\tan }^{-1}}\dfrac{a-b}{a+b}\] ....

Write the value of tan⁡−1ab−tan⁡−1a−ba+b{{\tan }^{-1}}\dfrac{a}{b}-{{\tan }^{-1}}\dfrac{a-b}{a+b} .

Explanation

Solution

Hint: The above question is related to inverse trigonometric function and looking at the form of the equation, it is very clear that you have to use the formula tan⁡−1A−tan⁡−1B=tan⁡−1A−B1+AB{{\tan }^{-1}}A-{{\tan }^{-1}}B={{\tan }^{-1}}\dfrac{A-B}{1+AB} . After that you need to simplify the expression by taking the LCM and eliminating the possible terms. Finally you need to use the value tan⁡−11=45∘{{\tan }^{-1}}1=45{}^\circ to reach the final answer.

Complete step by step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at the graph of tan⁡−1x{{\tan }^{-1}}x as well.

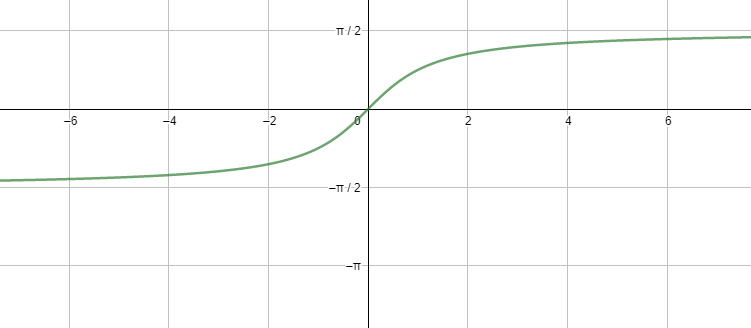
So, looking at the above graphs, we can draw the conclusion that tan⁡−1x{{\tan }^{-1}}x is defined for all real values of x, i.e., the domain of the function tan⁡−1x{{\tan }^{-1}}x is all real numbers while its range comes out to be (−π2,π2)\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right) .
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
tan⁡−1ab−tan⁡−1a−ba+b{{\tan }^{-1}}\dfrac{a}{b}-{{\tan }^{-1}}\dfrac{a-b}{a+b}
Now, we know tan⁡−1A−tan⁡−1B=tan⁡−1A−B1+AB{{\tan }^{-1}}A-{{\tan }^{-1}}B={{\tan }^{-1}}\dfrac{A-B}{1+AB} , we get
tan⁡−1ab−a−ba+b1+a(a−b)b(a+b){{\tan }^{-1}}\dfrac{\dfrac{a}{b}-\dfrac{a-b}{a+b}}{1+\dfrac{a\left( a-b \right)}{b\left( a+b \right)}}
=tan⁡−1(a(a+b)−b(a−b)b(a+b)b(a+b)+a(a−b)b(a+b))={{\tan }^{-1}}\left( \dfrac{\dfrac{a\left( a+b \right)-b(a-b)}{b\left( a+b \right)}}{\dfrac{b(a+b)+a\left( a-b \right)}{b\left( a+b \right)}} \right)
=tan⁡−1(a2+ab−ab+b2a2+b2+ab−ab)={{\tan }^{-1}}\left( \dfrac{{{a}^{2}}+ab-ab+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}+ab-ab} \right)
=tan⁡−1(a2+b2a2+b2)={{\tan }^{-1}}\left( \dfrac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}} \right)
=tan⁡−11={{\tan }^{-1}}1
We know that the value of tan⁡−11{{\tan }^{-1}}1 is equal to π4\dfrac{\pi }{4} . So, we can say that that the value of tan⁡−1ab−tan⁡−1a−ba+b{{\tan }^{-1}}\dfrac{a}{b}-{{\tan }^{-1}}\dfrac{a-b}{a+b} comes to be equal to π4\dfrac{\pi }{4} .

Note: Be careful about the signs in the formula tan⁡−1A−tan⁡−1B=tan⁡−1A−B1+AB{{\tan }^{-1}}A-{{\tan }^{-1}}B={{\tan }^{-1}}\dfrac{A-B}{1+AB} , as students many a times get confused and take the formula as tan⁡−1A−tan⁡−1B=tan⁡−1A+B1−AB{{\tan }^{-1}}A-{{\tan }^{-1}}B={{\tan }^{-1}}\dfrac{A+B}{1-AB} . Remembering the domain and range of the trigonometric inverse function tan⁡−1x{{\tan }^{-1}}x is very important.