Question

Write the statement of Gauss' law for electrostatics. Draw a diagram and derive an expression for the electric field due to a uniformly charged infinite plane sheet at a point near the sheet. For the given diagram, write the value of electric flux passing through the surface.

Answer 1

The Gauss’s law relates the distribution of electric charge and the resulting electric field. To apply Gauss's law, we have to understand the quantity known as electric flux which is the integral of the electric field and area.

Complete step by step answer:
Part 1: Gauss’s law of electrostatics:
Gauss’ law gives a relationship between the electric flux through a closed surface and the amount of charge enclosed by it. For the expression of electric field due to a uniformly charged infinite plane sheet use gauss’ law around a cylindrical surface.
Gauss law for electrostatics states that total electric flux through a closed surface is the same as the enclosed charge by the surface divided by the permittivity of the medium. Mathematically:
${\Phi _E} = \oint {\vec E.d\vec S = \dfrac{{{Q_{enc}}}}{\varepsilon_0 }}$
Where,
${\Phi _E}$ is the amount of electric flux,
$\vec E$ is electric field,
$d\vec S$ is very tiny surface element,
${Q_{enc}}$ is total charge enclosed by the closed surface,
$\varepsilon_0$ is the permittivity of the medium.

Part 2

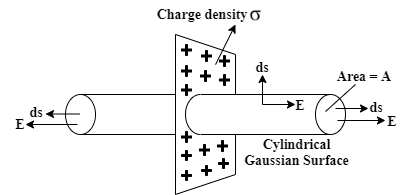
Let, Surface charge density of the sheet is $\sigma$. Now, consider a cylindrical Gaussian surface which is passing through the surface. As shown in the figure, it’s both end surface has an area A. At any point in front of the plane, the direction of the electric field $\vec E$will be perpendicularly outward from the plane. Notice, for the curved surface of the cylinder the direction of the surface element is always perpendicularly out of the plane, hence perpendicular to $\vec E$also. But on both planes they are aligned. So, applying gauss law you’ll get:
$\oint {\vec E.d\vec S = \dfrac{{\sigma .A}}{\varepsilon_0 }}$
$\Rightarrow EA + EA = \dfrac{{\sigma A}}{\varepsilon_0 }$
$\Rightarrow 2E = \dfrac{\sigma }{\varepsilon_0 }$
$\therefore E = \dfrac{\sigma }{{2\varepsilon_0 }}$
So, for an infinite charged sheet electric field is $\dfrac{\sigma }{{2\varepsilon_0 }}$acting perpendicularly outward from the plane.

Part 3

In the given diagram, total charge inside the closed surface is ${Q_{enc}} = 2 + ( - 1)\mu C = 1\mu C$, Also using the value of permittivity in vacuum in gauss law you will get: $\mu C$.
Hence, the value of flux passing through the surface is approximately $1.13 \times {10^5}V.m$.

Note: Although gauss law is valid for any kind of closed surface, but for practical application of gauss law you always need to be very careful about choosing the type of Gaussian surface. Otherwise, executing the surface integral becomes too hard. So, to make life easier choose the Gaussian surface wisely.