Question

Write the relation between focal length and radius of curvature of a spherical mirror.

Answer 1

Hint : Before stating the relation, derive the relation between the radius of curvature and the focal length of a mirror. This will help you understand better. Use the fact that when a parallel ray of light drops on a concave mirror, it passes through the focus of the mirror after reflection.

Complete step by step answer
The relation between focal length $\left( f \right)$ and radius of curvature $\left( R \right)$ of a spherical mirror is that the focal length is equal to half of the radius of curvature i.e. $f = \dfrac{R}{2}$ .
Let us derive this relation
Consider a concave mirror such that its radius of curvature is very much larger than the diameter of its aperture.
We can take help from the figure given.

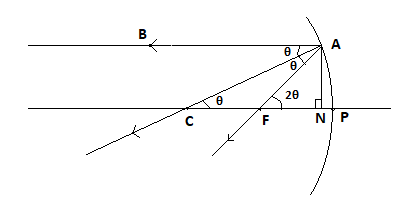
Suppose a parallel ray of light is incident on the mirror as shown in the figure. Let this incident ray make an angle $\theta$ with normal to the surface of the mirror. Since this mirror is part of a circle, the normal drawn to the surface of the circle passes through the center $\left( C \right)$ of the mirror.
We know that rays of light parallel to the principal axis passing through the focus $\left( F \right)$ of a concave mirror, after reflection.
Since the law of reflection says that the angle of incidence and angle of reflection are equal.
Therefore, $\angle BAC = \angle FAC = \theta$ as shown in the given figure.
Since BA and PC are parallel, $\angle BAC = \angle ACF = \theta$ .
Therefore, from the exterior angle theorem $\angle AFN = \angle ACF + \angle CAF = 2\theta$
Now drop a normal CP from point A. Let the foot of this normal be N.
Here, $\tan \theta = \dfrac{{AN}}{{CN}} \Rightarrow AN = CN\tan \theta$ ............ $\left( 1 \right)$
$\Rightarrow \tan 2\theta = \dfrac{{AN}}{{FN}} \Rightarrow AN = FN\tan 2\theta$ ............. $\left( 2 \right)$
From equation $\left( 1 \right)$ and equation, $\left( 2 \right)$ we get,
$CN\tan \theta = FN\tan 2\theta$
$\Rightarrow \dfrac{{CN}}{{FN}} = \dfrac{{\tan 2\theta }}{{\tan \theta }}$ ............... $\left( 3 \right)$
Meanwhile, the radius of curvature is very much greater than the diameter of its aperture, NP is very small compared to $CN$ and $CP$ and $\theta$ will be a small angle.
Therefore, $CN \approx CP$ and $FN \approx FP$ .
For small angles $\tan \theta = \theta$ and $\tan 2\theta = 2\theta$ .
Therefore, the equation $\left( 3 \right)$ can be written as
$\Rightarrow \dfrac{{CP}}{{FP}} = \dfrac{{2\theta }}{\theta }$
$\Rightarrow FP = \dfrac{{CP}}{2}$
And $CP = R$ and $FP = f$ .
Hence, $f = \dfrac{R}{2}$.

Note
Note that this relation between the radius of curvature $\left( R \right)$ of a concave mirror and the focal length $\left( f \right)$ of the mirror, which is $f = \dfrac{R}{2}$ , is true only when the $R$ is much greater than the diameter of its aperture.