Question
Question: Write the points of non-differentiability of \(f(x) = \left| {\log \left| x \right|} \right|\)....
Write the points of non-differentiability of f(x)=∣log∣x∣∣.
Solution
Hint: Here, we will plot the graph of the given function and find the points which are non-differentiable i.e., the points where the curve is changing its definition.
Complete step-by-step answer:
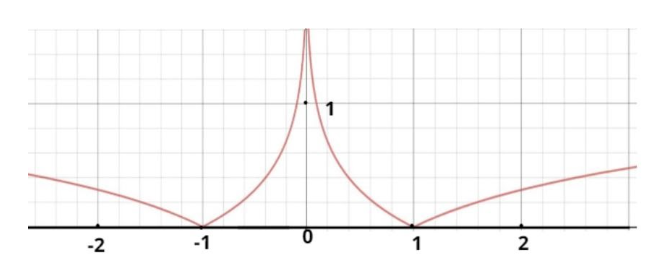
Now we have to find the points of non-differentiability of
f(x)=∣log∣x∣∣
Now we know that the modulus function is an absolute function hence we can say that f(x)=∣log∣x∣∣ will also be an absolute function
Now above graph depicts f(x)=∣log∣x∣∣
Clearly we can see from the graph that our f(x) is continuous everywhere but however it is non-differentiable at points x=−1 and x=1 because the curve is changing its definition at these two depicted points.
Hence x=±1 are the points where our f(x)=∣log∣x∣∣ is non-differentiable.
Note: While solving such problems it is always advisable to have great knowledge of graphs as it helps saving a lot of time during solving a question in entrance exams.
