Question

Write the formula to get the refractive index of the prism and write the terms in it.

Answer 1

Hint Draw a ray diagram showing the refraction inside and outside a prism. Use exterior angle property, angle sum property of a triangle and a quadrilateral and hence find a relation between incident angle, angle of deviation, and prism angle. Consider the ray of light to undergo a minimum angle of deviation and approximate the incident angle and emergent angle. Finally, substitute the derived value of incident and refracted angle into Snell’s law.

Complete step by step answer:

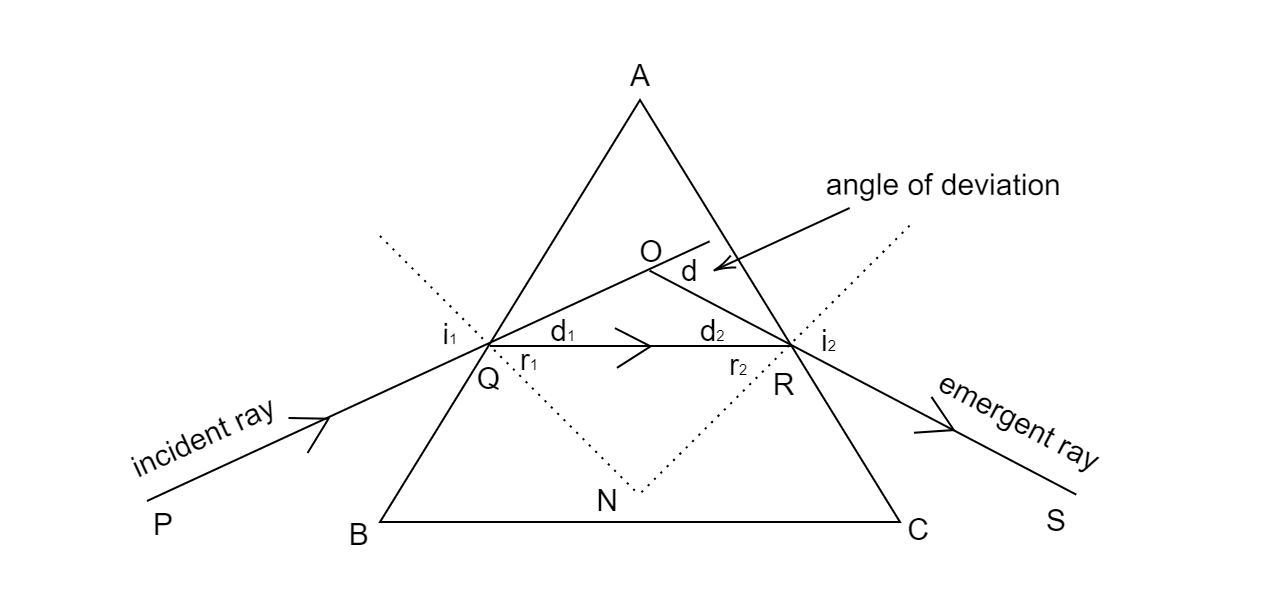
Let us consider a prism $ABC$ with a refractive index $\mu$. Let $QN$ and $RN$ be normal lines to the faces $AB$ and $AC$ respectively. Let the incident angle on the face $AB$ be ${{i}_{1}}$ and the refracted angle on this face be ${{r}_{1}}$. Let the incident angle on the face $AC$ be ${{r}_{2}}$ and the refracted ray after passing through $AC$ be ${{i}_{2}}$. We will extend the ray lines- $PQ$ and $SR$ to the point $O$. Let the angle of deviation be $d$.
In the quadrilateral $AQNR$, the sum of all four angles must be ${{360}^{\circ }}$ .
$\therefore \angle A+\angle N+\angle AQN+\angle ARN={{360}^{\circ }}$
But here, $\angle AQN=\angle ARN={{90}^{\circ }}$ as they are normal rays.
$\Rightarrow \angle A+\angle N=360-180$
Rearranging the above equation gives us
$\angle A=180-\angle N$
$\Rightarrow \angle A$ is an exterior angle in the triangle, $\Delta QRN$ .
Therefore, using the exterior angle property for the triangle $\Delta QRN$ gives us ${{r}_{1}}+{{r}_{2}}=A$ .
From the figure, let ${{i}_{1}}-{{r}_{1}}={{d}_{1}}$ and ${{i}_{2}}-{{r}_{2}}={{d}_{2}}$
By using the exterior angle property for the triangle $\Delta QOR$ ,
${{d}_{1}}+{{d}_{2}}=d$
By substituting ${{d}_{1}}$ as ${{i}_{1}}-{{r}_{1}}$ and ${{d}_{2}}$ as ${{i}_{2}}-{{r}_{2}}$, we get
${{i}_{1}}-{{r}_{1}}+{{i}_{2}}-{{r}_{2}}=d$
But we have already proved that ${{r}_{1}}+{{r}_{2}}=A$,
$\Rightarrow d={{i}_{1}}+{{i}_{2}}-A$
In the case of minimum deviation, ${{i}_{1}}\approx {{i}_{2}}\approx i$ and $d={{d}_{m}}$ .
Substituting these values in the above equation, we get
$i=\dfrac{A+{{d}_{m}}}{2}$
Now let us write Snell’s law for the prism,
$\mu =\dfrac{\sin i}{\sin r}$
From the already calculated values of $i$ and $r$, we get
$\mu =\dfrac{\sin \left( \dfrac{A+{{d}_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$
This is the equation of the refractive index for a prism with the prism angle - $A$ and angle of minimum deviation -${{d}_{m}}$ .

Note
A minimum angle of deviation in a prism means that the incident and the emergent angles will be equal, the refracted angles inside will be equal and the refracted ray will run parallel to the base of the prism. We use Snell’s law as the medium is getting changed.