Question

Write the formula to find the area of the sector of angle $\theta$ of a circle with radius r.

Answer 1

Hint: First, we have to draw a circle with center and radius as r. Then, we should know that the angle of the sector is $360{}^\circ$ and the area of the sector is $=\pi {{r}^{2}}$ . Thus, area of sector assuming angle as $1{}^\circ$ given by $=\dfrac{\pi {{r}^{2}}}{360{}^\circ }$ So, using unitary method we can find out area of sector having angle $\theta$.

Complete step by step answer:
Here, we will draw a circle with the center having radius r.

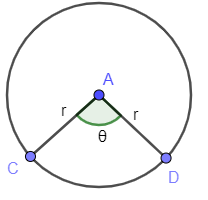
Angle of sector CAD is supposed to be $\theta$ . Now, in a circle with radius r and centre at A, $\angle CAD=\theta$ (in degrees) be the angle of the sector.
Then, the area of the sector of the circle is calculated using a unitary method.
We know that the angle of the sector is a total of $360{}^\circ$ . Area of sector i.e. the whole circle is $=\pi {{r}^{2}}$ .
So, it can be said that when the angle is $1{}^\circ$ , area of sector will be $=\dfrac{\pi {{r}^{2}}}{360{}^\circ }$ . Then, if the angle is $\theta$ what will be the area of the sector.
Now, using unitary method, we get equation as
$\begin{aligned} & 1{}^\circ =\dfrac{\pi {{r}^{2}}}{360{}^\circ } \\\ & \theta =? \\\ \end{aligned}$
On further solving, we get as
$=\dfrac{\pi {{r}^{2}}}{360{}^\circ }\times \theta$
On rearranging the terms, we can write it as
$=\dfrac{\theta }{360{}^\circ }\times \pi {{r}^{2}}$
Thus, the formula to find the area of the sector of angle $\theta$ of a circle with radius r is $\dfrac{\theta }{360{}^\circ }\times \pi {{r}^{2}}$ .

Note: Students sometimes make mistakes while not dividing angle with $360{}^\circ$ and directly multiplying given angle $\theta$ with area of circle. So, the formula to find the area of the sector will be equal to $=\theta \pi {{r}^{2}}$ which is wrong. Solving this means the area of the circle has only angle $\theta$ instead of $360{}^\circ$ . So, please understand the concept clearly and avoid making these types of mistakes.