Solveeit Logo
Login

Question

Question: Write the formula for finding volume of a frustum of a cone....

Write the formula for finding volume of a frustum of a cone.

Explanation

Solution

Hint: Find the frustum of a cone’s shape. From that you can observe the shape’s volume. So, subtracting the volume of the small cone from the volume of the total cone we can get the volume of frustum of the cone. Use normal geometry, find the relation between the angles in the cone. From that relate the volumes of both the cones. From that relation try to find differences between them. From the shape of frustum, you can say that the difference between volumes is nothing but volume of frustum.

Complete step-by-step answer:
When a solid is cut in such a manner that the base of the solid and the plane cutting the solid are parallel to each other, part of the solid which remains between the parallel cutting planes is known as frustum.
Frustum of cone is shown below.

Volume of frustum

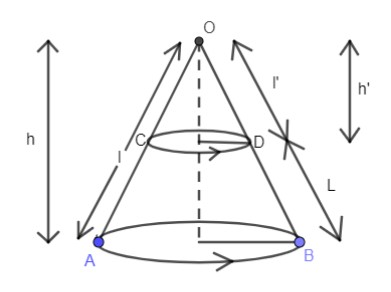
Let the large cone which has a height equal to h units, slant height as l units and radius as r units be named as cone 1 and smaller right cone be names as cone 2, whose height is given as h’ units, radius as r’ units, slant height is given as l’ units.
The height of Frustum is H and its slant height is L.
The volume of right circular cone 1 =13πr2h=\dfrac{1}{3}\pi {{r}^{2}}h
Volume of right circular cone 2 =13πr′2h′=\dfrac{1}{3}\pi r{{'}^{2}}h'
Volume of frustum of cone is given by subtracting total volume of cone and small right circular cone.
i.e Volume of cone 1-Volume of cone 2
Volume of frustum 13π(r2h−r′2h′)\dfrac{1}{3}\pi \left( {{r}^{2}}h-r{{'}^{2}}h' \right)
From figure ΔOO′D\Delta OO'D , ΔOPB\Delta OPB are similar from AA criterion.
⇒h′h=r′r\Rightarrow \dfrac{h'}{h}=\dfrac{r'}{r} . By substituting this into volume equation, we get:
V=13π(r2(h′rr′)−r′2h′)=13πh′(r3−r′3r′)V=\dfrac{1}{3}\pi \left( {{r}^{2}}\left( \dfrac{h'r}{r'} \right)-r{{'}^{2}}h' \right)=\dfrac{1}{3}\pi h'\left( \dfrac{{{r}^{3}}-r{{'}^{3}}}{r'} \right)
We know h=H+h′h=H+h'
Substituting this, we get:
h′H+h′=r′r\dfrac{h'}{H+h'}=\dfrac{r'}{r}
h′H=r′r−r′\dfrac{h'}{H}=\dfrac{r'}{r-r'}
h′=H(r′r−r′)h'=H\left( \dfrac{r'}{r-r'} \right)
Substituting the value of h’ in volume equation, we get:
V=13πH(r′r−r′)(r3−r′3r′)V=\dfrac{1}{3}\pi H\left( \dfrac{r'}{r-r'} \right)\left( \dfrac{{{r}^{3}}-r{{'}^{3}}}{r'} \right)
By cancelling the common terms in the above equation, we get:
V=13πH(r3−r′3r−r′)V=\dfrac{1}{3}\pi H\left( \dfrac{{{r}^{3}}-r{{'}^{3}}}{r-r'} \right)
By using general algebraic identity:
a3−b3=(a−b)(a2+ab+b2){{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)
By substituting above equation, we get:
V=13πH((r−r′)(r2+r′r+r′2)r−r′)V=\dfrac{1}{3}\pi H\left( \dfrac{\left( r-r' \right)\left( {{r}^{2}}+r'r+r{{'}^{2}} \right)}{r-r'} \right)
By cancelling common terms, we get:
V=13πH(r2+r′r+r′2)V=\dfrac{1}{3}\pi H\left( {{r}^{2}}+r'r+r{{'}^{2}} \right)
This gives the required volume of frustum of cone.

Note: Be careful in definition of frustum of cone, it is the part below not the cone part above. Be careful while getting relation between the H, h’ as this turns the volume simpler. If you miss the ′−′'-' sign r−r′r-r' will not get canceled and the answer may look very large. As here we don’t know the final answer each step must be calculated carefully. While finding the volume of a smaller cone take care of height and radius correspondingly.