Question

Write the following relation as set of ordered pairs and find which of them are functions:
$\\{ (x,y):x + y = 3,x,y \in (0,1,2,3)\\}$

Answer 1

In this question we have to write the set of ordered pairs by using the given relation and also we have to find whether the relationship is a function or not. Here we have that given relation only. So first we have to write the set ordered pairs by tracking the two numbers in the given relation. After that we have to check whether the given relation is a function or not.

Complete step-by-step answer:
The given function is: $\\{ (x,y):x + y = 3,x,y \in (0,1,2,3)\\}$
We have to find the ordered pair from the given set.
The given set is $(0,1,2,3)$
An ordered pair is a simple way of keeping track of two numbers by writing them in a specific order. The order of the numbers in the pair is important: x always comes before y.
From the given set, we will take the elements which will satisfy the condition $x + y = 3$.
We will take those elements as the ordered pair.
We can interchange the element and get other ordered pairs also.
To find the ordered pair means we have to find two number from the given set as $x \& y$ such that it satisfies $x + y = 3$
So, we have,
$0 + 0 \ne 3$, so $(0,0)$ is not the ordered pair.
$0 + 1 \ne 3$, so $(0,1)$ is not the ordered pair.
$0 + 2 \ne 3$, so $(0,2)$ is not the ordered pair.
$0 + 3 = 3$, so $(0,3)$ is the ordered pair.
$1 + 1 \ne 3$, so $(1,1)$ is not the ordered pair.
$1 + 2 = 3$, so $(1,2)$ is the ordered pair.
$1 + 3 \ne 3$, so $(0,1)$ is not the ordered pair.
$2 + 2 \ne 3$, so $(2,2)$ is not the ordered pair.
$2 + 3 \ne 3$, so $(2,3)$ is not the ordered pair.
Hence, the ordered pairs are: $(0,3)$, $(1,2)$,$(2,1)$, $(3,0)$
Now we have to find which of them are function,
Given relation is, $\\{ (x,y):x + y = 3,x,y \in (0,1,2,3)\\}$
Consider $A = (0,1,2,3)$,
Let us now define a mapping $f$ using the relation in given as $f:A \to A$ such that $f\left( x \right) = 3 - x$ where $x$ belongs to $A$. If the set formed using the above equation is well defined we can say it as a function. To say the defined mapping is well defined we have to prove it as a one-one function.

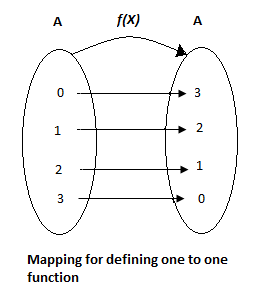
From the figure mapping for defining one to one function we can say that the defined mapping is well defined. Hence it is a function.

Note: While defining the order pairs we should note that $\left( {0,3} \right)$ is not equal to $\left( {3,0} \right)$ suppose we have $\left( {n,n} \right)$ $n$ times in a ordered pair we consider them as only one pair that is if we have $\left( {1,1} \right)$ two times we take them only once.
Also we should define the mapping from the given relation only, we should not use some other unrelated mappings.
Also we can define the mapping using $y$ such that $f\left( y \right) = 3 - y$ but the results remains unchanged