Question

Write the expression for electric intensity at a point due to a point charge and explain the terms.

Answer 1

The force of attraction between two static electric charges is given by Coulomb’s law. The electric intensity or electric field intensity of a charge is directly proportional to this force of attraction. Both force of attraction as well as electric field intensity are vectors.
Formula used: $\vec{F}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{r}^{2}}}\hat{r}$;
$\vec{E}=\dfrac{{\vec{F}}}{q}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{r}^{2}}q}\hat{r}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}\hat{r}$

_Complete step by step solution: _
Let us consider a point charge $Q$ located at a distance $r$ from another point charge $q$. The force of attraction between these two charges is given by Coulomb’s law as follows.
$\vec{F}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{r}^{2}}}\hat{r}$
Here,
$\vec{F}$ is the force of attraction between the charges $Q$ and $q$ separated by a distance $r$ as shown in the figure.
${{\varepsilon }_{0}}$ is the electric permittivity of free space.
$\hat{r}$ is the unit vector directed from $Q$ to $q$.

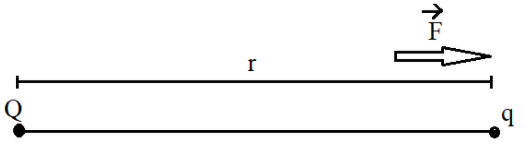
Let this be equation 1.
The electric field intensity due to $Q$ at the point where $q$ is placed is given by
$\vec{E}=\dfrac{{\vec{F}}}{q}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Qq}{{{r}^{2}}q}\hat{r}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{r}^{2}}}\hat{r}$
where $\vec{\underset{\scriptscriptstyle\centerdot}{E}}$ is the electric intensity or electric field intensity. Let this be equation 2.

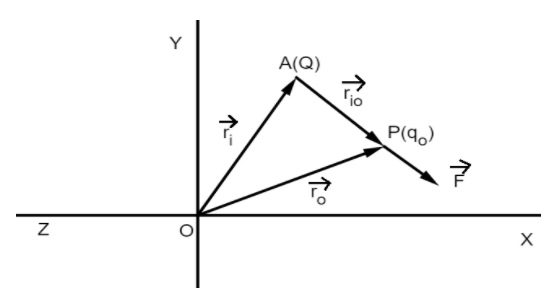
Now, let us see how the equations change when we consider a point charge in a three-dimensional space. Suppose the point charge $Q$ is located at a point $A$, in such a way that $\overrightarrow{OA}=\overrightarrow{{{r}_{i}}}$ as shown in the figure. We have to calculate the electric field intensity $(\overrightarrow{E})$ at a point $P$, where $\overrightarrow{OP}=\overrightarrow{{{r}_{o}}}$.
Firstly, let us place a small test charge ${{q}_{0}}$ at the point $P$. According to Coulomb’s law, we have
$\vec{F}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q{{q}_{0}}}{{{r}_{io}}^{2}}{{\hat{r}}_{io}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q{{q}_{0}}}{{{r}_{io}}^{3}}\overrightarrow{{{r}_{io}}}$
where
${{\hat{r}}_{io}}=\dfrac{\overrightarrow{{{r}_{io}}}}{{{r}_{io}}}$ is the unit vector directed from $A$ to $P$ as shown in the figure.
Let this be equation 3.
It is also clear from the figure that
$\overrightarrow{{{r}_{io}}}=\overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}}=\overrightarrow{AP}$
where
$\overrightarrow{{{r}_{io}}}$ is the distance between point $A$ and point $P$.
Let this be equation 4
Substituting equation 4 in equation 3, we have
$\vec{F}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q{{q}_{0}}}{{{r}_{io}}^{3}}\overrightarrow{{{r}_{io}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q{{q}_{0}}}{{{\left| \overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}} \right|}^{3}}}(\overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}})$
Let this be equation 5.
Now, the equation of electric field intensity due to a point charge $Q$ is given in equation 2.
Applying the same method in this three-dimensional space, we have
$\vec{E}=\dfrac{{\vec{F}}}{{{q}_{0}}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}{{q}_{0}}}\dfrac{Q{{q}_{0}}}{{{\left| \overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}} \right|}^{3}}}(\overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}})=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{\left| \overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}} \right|}^{3}}}(\overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}})$
Rewriting, the electric field intensity due to the point charge $Q$ is given by
$\overrightarrow{E}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{{{\left| \overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}} \right|}^{3}}}(\overrightarrow{{{r}_{o}}}-\overrightarrow{{{r}_{i}}})$
This electric field intensity is produced along $AP$.
This is how the electric intensity due to a point charge is derived.

Note: The magnitude of the electric intensity $\overrightarrow{E}$ due to a point charge $\overrightarrow{Q}$ depends only on the distance $r$. Hence, the electric field intensity due to a point charge is the same at equal distances. If we consider a point charge located at the center of a sphere, the electric field intensity at all the points on the surface of the sphere will be the same. We say that electric field intensity due to a point charge is spherically symmetric.