Question

Write the equation for the parabola and draw the graph.
Vertex $\left( 4,3 \right)$, axis of symmetry $y=3$, measure of latus rectum =$4,a>0$.

Answer 1

Assume the equation of the parabola as $x=a{{y}^{2}}+by+c$. Substitute the point $\left( 4,3 \right)$ in the parabola to form the first relation in a, b and c. Now, differentiate the equation of parabola and at the point $\left( 4,3 \right)$ substitute $\dfrac{dy}{dx}=\infty$ to form a second relation. Convert $x=a{{y}^{2}}+by+c$ in the form $\dfrac{1}{a}\left( x+\dfrac{D}{4a} \right)={{\left( y+\dfrac{b}{2a} \right)}^{2}}$ and compare it with ${{y}^{2}}=4Ax$. Use the formula : $L=\left| 4A \right|$ to determine the length of the latus rectum. Find the value of a using this and use the other two relations to find the value of b and c. Finally substitute them in $x=a{{y}^{2}}+by+c$ to get the answer.

Complete step-by-step solution:
We have been given that the axis of symmetry of parabola is $y=3$. So, let us assume the equation of parabola as $x=a{{y}^{2}}+by+c$. It is given that $a>0$, therefore the parabola will be opening rightwards.

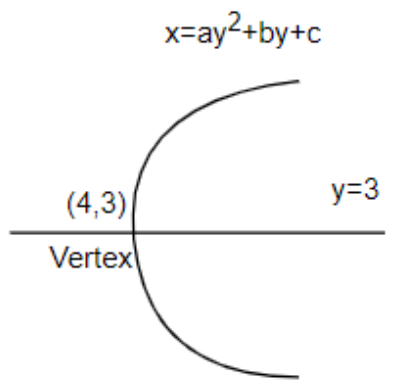
Now the vertex $\left( 4,3 \right)$ lies on the parabola, therefore substituting its value in the equation, we get,
$\Rightarrow 4=9a+3b+c\ldots \ldots \ldots \left( i \right)$
Also, we can clearly see that at point $\left( 4,3 \right)$ the slope of tangent $\left( \dfrac{dy}{dx} \right)$ to the parabola will be infinite as it will be perpendicular to x-axis. So, on differentiating the function, we get,
$\begin{aligned} & \Rightarrow 1=2ay\dfrac{dy}{dx}+b\dfrac{dy}{dx} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{1}{2ay+b} \\\ \end{aligned}$
Substituting $\dfrac{dy}{dx}=\infty$ at $\left( 4,3 \right)$, we get,
$\begin{aligned} & \Rightarrow \infty =\dfrac{1}{2ay+b} \\\ & \Rightarrow 2ay+b=\dfrac{1}{\infty }=0 \\\ & \Rightarrow 2a\times 3+b=0 \\\ & \Rightarrow 6a+b=0\ldots \ldots \ldots \left( ii \right) \\\ \end{aligned}$
Now, we know that $x=a{{y}^{2}}+by+c$ can be written in the whole square form by using the completing the square method. So, we have,
$x=a\left[ {{\left( y+\dfrac{b}{2a} \right)}^{2}}-\dfrac{D}{4{{a}^{2}}} \right]$
Here, $D={{b}^{2}}-4ac$ = discriminant of the quadratic equation.
$\begin{aligned} & \Rightarrow \dfrac{x}{a}+\dfrac{D}{4{{a}^{2}}}={{\left( y+\dfrac{b}{2a} \right)}^{2}} \\\ & \Rightarrow {{\left( y+\dfrac{b}{2a} \right)}^{2}}=\dfrac{1}{a}\left( x+\dfrac{D}{4a} \right) \\\ \end{aligned}$
This can be written as ${{Y}^{2}}=4mX$, where $Y=\left( y+\dfrac{b}{2a} \right),X=\left( x+\dfrac{D}{4a} \right)$ and $4m=\dfrac{1}{a}$. So, on comparing the above relation with the general equation of parabola given as ${{y}^{2}}=4Ax$, we get,
Length of latus rectum = $L=\left| 4A \right|$
So, for ${{Y}^{2}}=4mX$, latus rectum will be :
$L=\left| 4m \right|=\left| \dfrac{1}{a} \right|$
It is given that measure of latus rectum is 4 and $a>0$, therefore removing the modulus sign, we get,
$\begin{aligned} & \Rightarrow 4=\dfrac{1}{a} \\\ & \Rightarrow a=\dfrac{1}{4} \\\ \end{aligned}$
So, substituting $a=\dfrac{1}{4}$ in equation (i) and (ii) and solving for b and c, we get,
$b=\dfrac{-3}{2}$ and $c=\dfrac{25}{4}$
Now, substituting the values of a, b and c in the equation of parabola, we have,
$x=\dfrac{{{y}^{2}}}{4}-\dfrac{3y}{2}+\dfrac{25}{4}$
Now, to draw the graph, we have to determine the points at which the parabola will cut the x and y-axis.
So, for parabola to cut the x-axis, y must be 0.
$\Rightarrow x=\dfrac{25}{4}$
And for the parabola to cut the y-axis, x must be 0.
$\begin{aligned} & \Rightarrow 0=\dfrac{{{y}^{2}}}{4}-\dfrac{3y}{2}+\dfrac{25}{4} \\\ & \Rightarrow {{y}^{2}}-6y+25=0 \\\ \end{aligned}$
Here $D={{6}^{2}}-4\times 25=-64<0$, therefore there will not be any real value of y. So, parabola will not cut y-axis.
So, the graph can be plotted as shown below.

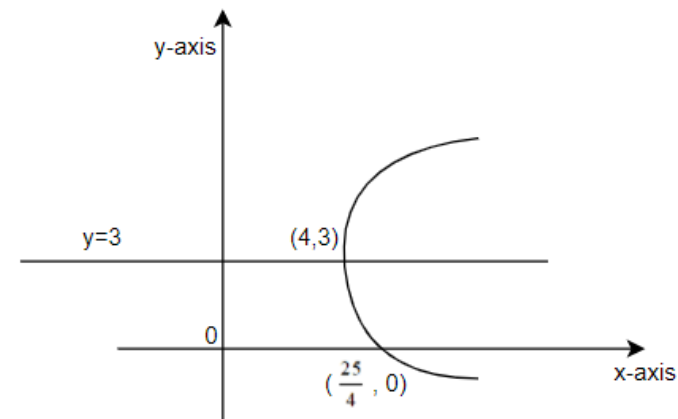
Note: One may note that there is an easy formula to solve the above question. The equation of parabola in vertex form is given as : $x=a{{\left( y-h \right)}^{2}}+k$, where $\left( h,k \right)$ is the vertex $\left( 4,3 \right)$. You may note an important thing that it is given that the axis of symmetry is $y=3$ and that is why we have assumed the equation of parabola as $x=a{{y}^{2}}+by+c$. If the axis of symmetry would have been y = constant, then we would have assumed the equation of parabola as $y=a{{x}^{2}}+bx+c$.