Question
Question: Write the equation for the parabola and draw the graph. Vertex \(\left( -7,4 \right)\), axis of sy...
Write the equation for the parabola and draw the graph.
Vertex (−7,4), axis of symmetry x=−7, measure of latus rectum 6,a<0.
Solution
Assume the equation of the parabola as y=ax2+bx+c. Substitute the point (−7,4) in the parabola to form the first relation in a, b and c. Now, differentiate the equation of parabola and at the point (−7,4) substitute dxdy=0 to form a second relation. Convert y=ax2+bx+c in the form a1(y+4aD)=(x+2ab)2 and compare it with x2=4Ay. Use the formula : L=∣4A∣ to determine the length of latus rectum. Find the value of a using this and use the other two relations to find the value of b and c. Finally substitute them in y=ax2+bx+c to get the answer.
Complete step-by-step solution:
We have been given that the axis of symmetry of parabola is x=−7. Let us assume the equation of parabola as y=ax2+bx+c. It is given that a<0, therefore the parabola will be opening downwards.
Now the vertex (−7,4) lies on the parabola, therefore substituting its value in the equation, we get,
⇒4=49a−7b+c………(i)
Also, we can clearly see that at point (−7,4) the slope of tangent (dxdy) to the parabola will be zero as it will be parallel to x-axis. So, on differentiating the function, we get,
⇒dxdy=2ax+b
Substituting dxdy=0 at (−7,4), we get,
⇒0=−14a+b⇒14a=b………(ii)
Now, we know that y=ax2+bx+c can be written in the whole square form by using the square method. So, we have,
y=a[(x+2ab)2−4a2D]
Here, D=b2−4ac = discriminant of the quadratic equation.
⇒ay+4a2D=(x+2ab)2⇒(x+2ab)2=a1(y+4aD)
This can be written as X2=4mY, where X=(x+2ab),Y=(y+4aD) and 4m=a1. So, on comparing the above relation with the general equation of parabola given as x2=4Ay, we get,
Length of latus rectum = L=∣4A∣
So, for X2=4mY, latus rectum will be :
L=∣4m∣=a1
It is given that measure of latus rectum is 6 and a<0, therefore removing the modulus sign, we get,
⇒6=a−1⇒a=6−1
So, substituting a=6−1 in equation (i) and (ii) and solving for b and c, we get,
b=3−7 and c=6−25
Now, substituting the values of a, b and c in the equation of parabola, we have,
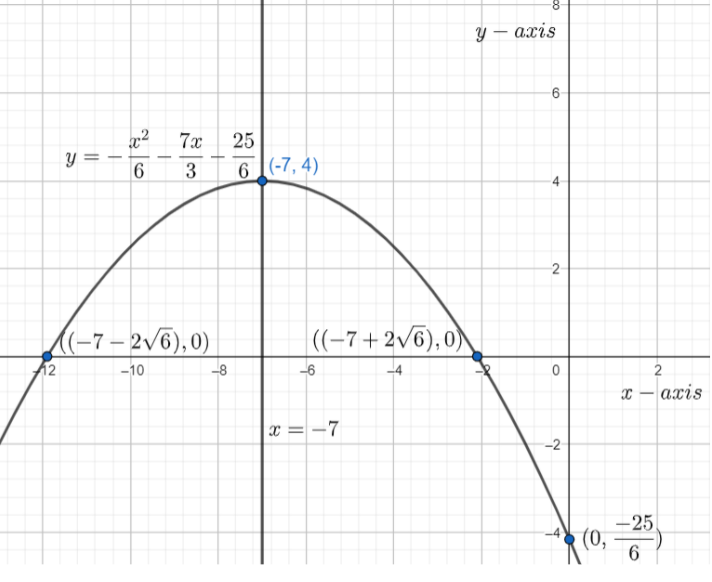
y=6−x2−37x−625
Now, to draw the graph, we have to determine the points at which the parabola will cut the x and y-axis.
So, for the parabola to cut the y-axis, x must be 0.
⇒y=6−25
And for parabola to cut x-axis, y must be 0.
⇒0=6−x2−37x−625⇒x2+14x+25=0⇒x=2−14±142−25×4⇒x=2−14±96⇒x=2−14±46∴x=−7+26 or −7−26
So, the graph can be plotted as shown below.
Note: One may note that there is an easy formula to solve the above question. The equation of parabola in vertex form is given as : y=a(x−h)2+k, where (h,k) is the vertex (−7,4). You may note an important thing that it is given that the axis of symmetry is x=−7 and that is why we have assumed the equation of parabola as y=ax2+bx+c. If the axis of symmetry would have been y = constant, then we would have assumed the equation of parabola as x=ay2+by+c.
